چکیده
Z3 یک حلکننده کارآمد نظریههای پیمانهای ارضاپذیری (SMT) است که توسط بخش تحقیقات مایکروسافت توسعه داده شده است. Z3 ابزار قدرتمندی برای حل مسائلی است که شامل ترکیبی از نظریههای پسزمینه مانند حساب، بردارهای بیتی، آرایهها و توابع تفسیر نشده هستند و به طور گسترده در تأیید، تحلیل و آزمایش نرمافزار استفاده میشوند. Z3 با استفاده از ادغام دقیق موتورهای تخصصی برای نظریههای مختلف و با بهرهگیری از تکنیکهای حل ارضاپذیری بولی (SAT) به کارایی دست مییابد. Z3 به صورت رایگان از Microsoft Research در دسترس است.
مقدمه
نظریههای پیمانهای ارضاپذیری (SMT) با افزودن استدلال برابری، حساب، بردارهای بیتی با اندازه ثابت، آرایهها، کمیتسنجها و سایر نظریههای مفید مرتبه اول، ارضاپذیری بولی (SAT) را تعمیم میدهند.
یک حلکننده SMT ابزاری است برای تصمیمگیری درباره قابلیت حل (satisfiability) یا بهطور معکوس اعتبار (validity) فرمولها در این نظریهها.
حلکنندههای SMT کاربردهایی مانند بررسی استاتیک پیشرفته (extended static checking)، انتزاع گزارهای (predicate abstraction)، تولید تستهای نرمافزاری و بررسی مدل محدود (bounded model checking) در حوزههای نامتناهی را ممکن میسازند، که چند مورد از آنها را ذکر میکنیم.
Z3 یک حلکنندهی جدید SMT از Microsoft Research است. این ابزار با هدف حل مسائلی که در تأیید و تحلیل نرمافزار مطرح میشوند، طراحی شده است. از این رو، Z3 از مجموعه متنوعی از نظریهها پشتیبانی میکند. یک نمونه اولیه از Z3 در SMT-COMP’07 شرکت کرد و موفق شد ۴ مقام اول و ۷ مقام دوم را کسب کند. Z3 از الگوریتمهای نوین برای نمونهسازی کمیت سنجها (quantifier instantiation) و ترکیب نظریهها (theory combination) استفاده میکند. اولین نسخه خارجی Z3 در سپتامبر ۲۰۰۷ منتشر شد. اطلاعات بیشتر، از جمله راهنمای دانلود و نصب این ابزار، در صفحه وب Z3 در دسترس است: Z3 Web Page. در حال حاضر، Z3 در پروژههایی مانند Spec#/Boogie، Pex، HAVOC، Vigilante، یک کامپایلر معتبر C (VCC) و Yogi استفاده میشود و در حال یکپارچهسازی با سایر پروژهها مانند SLAM/SDV است.
کلاینت
پیش از توضیح عملکرد داخلی Z3، دو مورد از کاربردهای منتخب آن بهطور کوتاه شرح داده میشوند.
Front-endها با Z3 از طریق فرمت متنی یا رابط برنامهنویسی باینری (API) تعامل دارند.
سه فرمت ورودی متنی پشتیبانی میشوند:
- فرمت SMT-LIB
- فرمت Simplify
- یک فرمت سطح پایین بومی مشابه فرمت DIMACS برای فرمولهای SAT منطقی بولی
همچنین میتوان Z3 را بهصورت رویهای (procedurally) فراخوانی کرد، با استفاده از:
- API زبان ANSI C
- API برای .NET managed common language runtime
- API زبان OCaml
Spec#/Boogie. شرایط تأیید منطقی را از یک برنامه Spec# یک افزونه C# تولید میکند. در داخل، از Z3 برای تجزیه و تحلیل شرایط تأیید، اثبات صحت برنامهها یا یافتن خطاها در آنها استفاده میکند. فرمولهای تولید شده توسط Spec#/Boogie حاوی کمیت سنجهای جهانی هستند و همچنین از حساب اعداد صحیح خطی استفاده میکنند.
Spec#. در ماه مه 2007، Z3 را به عنوان موتور استدلال پیشفرض جایگزین اثباتکننده قضیه Simplify کرد که منجر به بهبود قابل توجه عملکرد در طول اثبات قضیه شد. Pex Program EXploration یک دستیار هوشمند برای برنامهنویس است. با تولید خودکار تستهای واحد، امکان یافتن زودهنگام اشکالات را فراهم میکند. علاوه بر این، به برنامهنویس پیشنهاد میدهد که چگونه اشکالات را برطرف کند. Pex رفتار برنامه را از ردپاهای اجرا یاد میگیرد و Z3 برای تولید موارد آزمایشی جدید با رفتار متفاوت استفاده میشود. نتیجه یک مجموعه تست حداقلی با حداکثر پوشش کد است. فرمولهای تولید شده توسط Pex شامل بردارهای بیتی با اندازه ثابت، تاپلها، آرایهها و کمیت سنجها هستند.
معماری سیستم
Z3 یک حلکننده SAT مدرن مبتنی بر DPLL، یک حلکننده نظریه اصلی که برابریها و توابع تفسیر نشده را مدیریت میکند، حلکنندههای ماهوارهای (برای حساب، آرایهها و غیره) و یک ماشین انتزاعی تطبیق E برای کمیت سنجهارا ادغام میکند. Z3 با زبان C++ پیادهسازی شده است. نمای کلی شماتیک Z3 در شکل زیر نشان داده شده است.
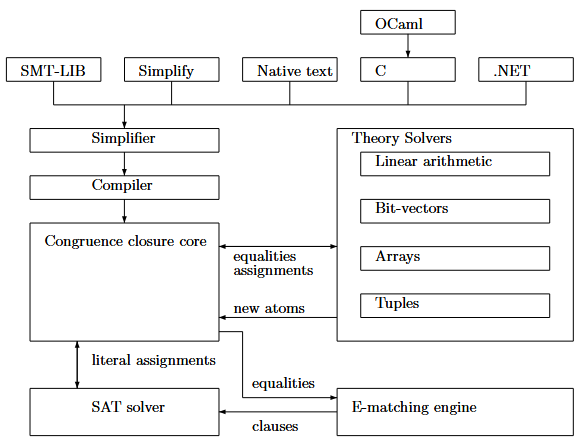
سادهساز. فرمولهای ورودی سادهساز ابتدا با استفاده از یک سادهسازی ناقص اما کارآمد پردازش میشوند. سادهساز، قوانین کاهش جبری استاندارد، مانند p ∧ true 7 → p را اعمال میکند، اما سادهسازی زمینهای محدودی را نیز انجام میدهد، زیرا تعاریف معادلهای را در یک زمینه شناسایی میکند و فرمول باقیمانده را با استفاده از تعریف کاهش میدهد، بنابراین برای مثال x = 4 ∧ q(x) 7 → x = 4 ∧ q(4). پیوستگی ارضاپذیر بدیهی x = 4 در هسته کامپایل نمیشود، اما در صورتی که کلاینت به مدلی برای ارزیابی x نیاز داشته باشد، کنار گذاشته میشود.
کامپایلر. نمایش درخت نحوی انتزاعی سادهشده فرمول به یک ساختار داده متفاوت متشکل از مجموعهای از بندها و گرههای بسته شدن همنهشتی تبدیل میشود.
هسته بسته شدن همنهشتی. هسته بسته شدن همنهشتی انتسابهای درستی به اتمها را از حلکننده SAT دریافت میکند. اتمها بر روی تساویها و فرمولهای اتمی خاص نظریه، مانند نابرابریهای حسابی، قرار دارند. تساویهای ادعا شده توسط حلکننده SAT توسط هسته بسته شدن همنهشتی با استفاده از یک ساختار داده که ما آن را گراف E در ادامه [8] مینامیم، منتشر میشوند. گرههای موجود در گراف E ممکن است به یک یا چند حلکننده نظریه اشاره کنند. هنگامی که دو گره ادغام میشوند، مجموعه مراجع حلکننده نظریه ادغام میشوند و ادغام به عنوان یک تساوی به حلکنندههای نظریه در تقاطع دو مجموعه مراجع حلکننده منتشر میشود. هسته همچنین اثرات حلکنندههای نظریه، مانند تساویهای استنباطی که تولید میشوند و اتمهایی که به درست یا غلط اختصاص داده میشوند را منتشر میکند. حلکنندههای نظریه همچنین ممکن است در مورد نظریههای غیر محدب، اتمهای جدیدی تولید کنند. این اتمها متعاقباً متعلق به حلکننده SAT هستند و به آنها اختصاص داده میشوند.
ترکیب نظریه: روشهای سنتی برای ترکیب حلکنندههای نظریه به قابلیتهای حلکنندهها برای تولید تمام تساویهای ضمنی یا یک مرحله پیشپردازش که لیترالهای اضافی را به فضای جستجو وارد میکند، متکی هستند. Z3 از یک روش جدید ترکیب نظریه استفاده میکند که به صورت افزایشی مدلهای نگهداری شده توسط هر نظریه را تطبیق میدهد [5].
حلکننده SAT. تقسیمهای حالت بولی با استفاده از یک حلکننده SAT پیشرفته کنترل میشوند. حلکننده SAT روشهای استاندارد هرس جستجو، مانند لیترالهای دو-ساعته برای انتشار کارآمد محدودیت بولی، یادگیری لم با استفاده از بندهای تعارض، ذخیرهسازی فازی برای هدایت تقسیم حالتها را ادغام میکند و عقبگرد غیر-زمانی را انجام میدهد.
حذف بندها. نمونهسازی کمیتسنج دارای یک اثر جانبی است که بندهای جدیدی حاوی اتمهای جدید را در فضای جستجو تولید میکند. Z3 بندهایی را که در بستن شاخهها بیفایده بودند، به همراه اتمها و عباراتشان، جمعآوری میکند. از سوی دیگر، بندهای تعارض و حروف استفاده شده در آنها حذف نمیشوند، بنابراین نمونههای کمیتسنج که در ایجاد تعارض مفید بودند، به عنوان یک اثر جانبی حفظ میشوند.
انتشار ارتباط. حلکنندههای مبتنی بر DPLL(T) یک مقدار بولی را به تمام اتمهای ظاهر شده در یک هدف اختصاص میدهند. در عمل، چندین مورد از این اتمها اهمیتی ندارند. Z3 این اتمها را به دلیل نظریههای پرهزینه، مانند بردارهای بیتی، و قوانین استنتاج، مانند نمونهسازی کمیتسنج، نادیده میگیرد. الگوریتم مورد استفاده برای تشخیص اتمهای مرتبط از غیر اهمیتی ندارد در [6] شرح داده شده است.
نمونهسازی کمیتسنج با استفاده از تطبیق E. Z3 از یک رویکرد شناخته شده برای استدلال کمیتسنج استفاده میکند که روی یک گراف E برای نمونهسازی متغیرهای کمی کار میکند. Z3 از الگوریتمهای جدیدی استفاده میکند که تطابقها را روی گرافهای E به صورت تدریجی و کارآمد شناسایی میکنند. نتایج تجربی بهبود عملکرد قابل توجهی را نسبت به حلکنندههای SMT پیشرفته موجود نشان میدهد [4].
حلکنندههای نظریه. Z3 از یک حلکننده حساب خطی مبتنی بر الگوریتم استفاده شده در Yices [9] استفاده میکند. نظریه آرایه از نمونهسازی تنبل از اصول موضوع آرایه استفاده میکند. نظریه بردارهای بیتی با اندازه ثابت، انفجار بیت را برای همه عملیات بردار بیتی اعمال میکند، اما برابری.
تولید مدل. Z3 توانایی تولید مدلها را به عنوان بخشی از خروجی دارد. مدلها مقادیر را به ثابتهای ورودی اختصاص میدهند و نمودارهای تابع جزئی را برای گزارهها و نمادهای تابع تولید میکنند.
نتیجهگیری
Z3 از فوریه 2007 در چندین پروژه در مایکروسافت مورد استفاده قرار گرفته است. کاربردهای اصلی آن بررسی استاتیک توسعهیافته، تولید حالت آزمایشی و انتزاع گزاره است.
منابع
1. T. Ball and S. K. Rajamani. The SLAM project: debugging system software via
static analysis. SIGPLAN Not., 37(1):1–3, 2002.
2. M. Barnett, K. R. M. Leino, and W. Schulte. The Spec# programming system:
An overview. In CASSIS 2004, LNCS 3362, pages 49–69. Springer, 2005.
3. M. Costa, J. Crowcroft, M. Castro, A. I. T. Rowstron, L. Zhou, L. Zhang, and
P. Barham. Vigilante: end-to-end containment of internet worms. In A. Herbert
and K. P. Birman, editors, SOSP, pages 133–147. ACM, 2005.
4. L. de Moura and N. Bjørner. Efficient E-matching for SMT Solvers. In CADE’07.
Springer-Verlag, 2007.
5. L. de Moura and N. Bjørner. Model-based Theory Combination. In SMT’07, 2007.
6. L. de Moura and N. Bjørner. Relevancy Propagation. Technical Report MSR-TR-
2007-140, Microsoft Research, 2007.
7. R. DeLine and K. R. M. Leino. BoogiePL: A typed procedural language for check-
ing object-oriented programs. Technical Report 2005-70, Microsoft Research, 2005.
8. D. Detlefs, G. Nelson, and J. B. Saxe. Simplify: a theorem prover for program
checking. J. ACM, 52(3):365–473, 2005.
9. B. Dutertre and L. de Moura. A Fast Linear-Arithmetic Solver for DPLL(T). In
CAV’06, LNCS 4144, pages 81–94. Springer-Verlag, 2006.
10. B. S. Gulavani, T. A. Henzinger, Y. Kannan, A. V. Nori, and S. K. Rajamani. Syn-
ergy: a new algorithm for property checking. In Michal Young and Premkumar T.
Devanbu, editors, SIGSOFT FSE, pages 117–127. ACM, 2006.
11. S. K. Lahiri and S. Qadeer. Back to the Future: Revisiting Precise Program Veri-
fication using SMT Solvers. In POPL’2008, 2008.
12. S. Ranise and C. Tinelli. The Satisfiability Modulo Theories Library (SMT-LIB).
www.SMT-LIB.org, 2006.
13. N. Tillmann and W. Schulte. Unit Tests Reloaded: Parameterized Unit Testing
with Symbolic Execution. IEEE software, 23:38–47, 2006.



