فازینگ جعبه‌ خاکستری هدایت ‌شده (Directed Greybox Fuzzing یا DGF) رویکردی مؤثر است که با استفاده از نقاط هدف از پیش‌ تعریف‌ شده، برای تقویت آزمون نواحی آسیب‌پذیر کد طراحی شده است. روش‌های پیشرفته DGF با بازتعریف و بهینه‌سازی معیار برازندگی (fitness metric) تلاش می‌کنند به‌صورت دقیق و سریع به نقاط هدف برسند. با این حال، بهینه‌ سازی‌های معیار برازندگی عمدتاً بر الگوریتم‌های ابتکاری متکی هستند که معمولاً به اطلاعات اجرای گذشته وابسته‌اند و دیدی نسبت به مسیرهایی که هنوز اجرا نشده‌اند ندارند. در نتیجه، مسیرهای دشوار برای اجرا که دارای قیود پیچیده‌اند می‌توانند مانع رسیدن DGF به اهداف شوند و کارایی آن را کاهش دهند.

ما در این مقاله، DeepGo را معرفی می‌کنیم؛ یک فازر جعبه ‌خاکستری هدایت ‌شده پیش‌بینانه (predictive directed grey-box fuzzer) که می‌تواند اطلاعات تاریخی و پیش‌بینی ‌شده را با هم ترکیب کند تا DGF را از طریق یک مسیر بهینه به نقطه هدف هدایت کند. ابتدا، مدل انتقال مسیر (path transition model) را پیشنهاد می‌دهیم که DGF را به‌عنوان فرایندی برای رسیدن به نقطه هدف از طریق دنباله‌های مشخص انتقال مسیر مدل‌سازی می‌کند. بذر (seed) جدیدی که در اثر جهش (mutation) تولید می‌شود باعث وقوع گذار مسیر می‌گردد، و مسیری که متناظر با توالی گذار مسیر با پاداش بالا است، نشان‌دهنده احتمال بالای رسیدن به نقطه هدف از طریق آن مسیر است.

سپس، برای پیش‌بینی گذارهای مسیر و پاداش‌های متناظر با آن‌ها، از شبکه‌های عصبی عمیق استفاده می‌کنیم تا محیط ترکیبی مجازی (Virtual Ensemble Environment یا VEE) را بسازیم؛ محیطی که به‌تدریج مدل گذار مسیر را تقلید کرده و پاداش گذارهایی را که هنوز طی نشده‌اند پیش‌بینی می‌کند. برای تعیین مسیر بهینه، یک مدل یادگیری تقویتی برای فازینگ (Reinforcement Learning for Fuzzing یا RLF) توسعه می‌دهیم تا توالی‌های گذار با بیشترین پاداش تجمعی را تولید کند. مدل RLF می‌تواند گذارهای مسیر تاریخی و پیش‌بینی‌شده را ترکیب کرده و توالی‌های گذار مسیر بهینه را به‌همراه سیاستی برای هدایت راهبرد جهش در فازینگ تولید کند.

در نهایت، برای اعمال توالی گذار مسیر با پاداش بالا، مفهوم گروه کُنش (action group) را معرفی می‌کنیم که مراحل کلیدی فازینگ را به‌صورت جامع بهینه‌سازی می‌کند تا مسیر بهینه برای رسیدن کارآمد به هدف محقق شود. ما DeepGo را روی دو مجموعه معیار شامل ۲۵ برنامه با مجموع ۱۰۰ نقطه هدف ارزیابی کردیم. نتایج آزمایش‌ها نشان می‌دهد که DeepGo در رسیدن به نقاط هدف به‌ترتیب نسبت به AFLGo، BEACON، WindRanger و ParmeSan بهبود سرعت ×3.23، ×1.72، ×1.81 و ×4.83 را به‌دست می‌آورد و در آشکارسازی آسیب‌پذیری‌های شناخته‌ شده نیز به‌ترتیب ×2.61, ×3.32, ×2.43 و ×2.53 افزایش سرعت دارد.

1. مقدمه

فازینگ جعبه ‌خاکستری هدایت ‌شده (Directed Greybox Fuzzing یا DGF) [9] یک تکنیک کارآمد است که برای آزمون نواحی آسیب‌پذیر کد طراحی شده است. با تعریف یک معیار برازندگی (fitness metric) قابل اندازه‌گیری، فازر جعبه‌ خاکستری هدایت‌شده می‌تواند بذرهای (seed) امیدوارکننده را انتخاب کرده و فرصت‌های جهش بیشتری به آن‌ها بدهد تا به‌تدریج به نقطهٔ هدف نزدیک شوند.

برای مثال، بر اساس اطلاعات گراف فراخوانی (Call Graph) و گراف جریان کنترل (Control-Flow Graph) برنامه تحت آزمون (Program Under Test یا PUT)، روش‌های رایج DGF از فاصلهٔ بین ورودی‌ها و نقاط هدف به‌ عنوان معیار برازندگی برای کمک به انتخاب بذر و تخصیص انرژی بذر استفاده می‌کنند. بذرهایی که به نقطهٔ هدف نزدیک‌تر هستند، به‌ عنوان بذرهای امیدوارکننده در نظر گرفته شده و در اولویت قرار می‌گیرند.

DGF بیشتر زمان خود را صرف رسیدن به این مکان‌ها می‌کند، بدون آنکه منابع را برای تحت فشار قرار دادن بخش‌های نامرتبط هدر دهد؛ بنابراین، این روش به‌ویژه برای سناریوهای آزمون مانند آزمون وصله (patch testing) [59]، بازتولید باگ [54] و اعتبارسنجی کدهای بالقوه معیوب [82] بسیار مناسب است.

برای تقویت جهت‌مندی و بهبود کارایی، پژوهش‌های پیشرفتهٔ DGF از روش‌های ابتکاری برای بازتعریف و بهینه‌سازی معیارهای برازندگی استفاده می‌کنند. برای نمونه، برخی تکنیک‌های DGF معیار برازندگی را بر اساس شباهت رد اجرا (مانند Hawkeye [15])، شرایط داده‌ای (مانند CAFL [40]) و اطلاعات جریان داده (مانند WindRanger [22]) بازتعریف می‌کنند. برخی فازرهای هدایت‌شده نیز از رویکردهای مبتنی بر توالی برای افزایش جهت‌مندی بهره می‌برند؛ مانند گسترش توالی هدف داده‌شده (مانند Berry [44]) و استفاده از توالی استفاده‌ پس‌ از‌ آزادسازی (use-after-free) به‌عنوان راهنما (مانند Lolly [30]). همچنین، برخی تکنیک‌های DGF با هرس مسیرهای غیرقابل‌دسترس به هدف (مانند BEACON [31]) و ساخت اوراکل قابل پرس‌وجو برای هدایت فازینگ (مانند MC² [67]) کارایی را بهبود می‌دهند.

با این حال، در فرایند فازینگ، جهش بذرها (mutation of seeds) موجب عدم قطعیت در مسیر اجرای برنامه می‌شود. روش‌های ابتکاری موجود معمولاً به اطلاعات اجرای تاریخی متکی هستند و فاقد توان پیش‌بینی مسیرهایی‌اند که تاکنون اجرا نشده‌اند. برای نمونه، هنگامی که فاصله در سطح بلاک پایه (Basic Block) تا نقطهٔ هدف به‌عنوان معیار برازندگی (Fitness Metric) استفاده می‌شود، بذرهایی با فاصلهٔ کوتاه‌تر در اولویت قرار می‌گیرند، بدون آن‌که امکان‌پذیری مسیر در نظر گرفته شود. در نتیجه، مسیرهای دشوار برای اجرا که دارای قیود پیچیده هستند، مانع از رسیدن فازینگ هدایت‌شدهٔ خاکستری (DGF) به نقاط هدف می‌شوند و کارایی آن را کاهش می‌دهند.

ازاین‌رو، در این مقاله هدف ما طراحی یک فازر خاکستری هدایت‌ شدهٔ پیش‌بینانه (Predicted Directed Greybox Fuzzer) است که قادر باشد اطلاعات حیاتی اجرای برنامه را پیش‌بینی کرده و مسیر بهینه را تخمین بزند. با ترکیب اطلاعات اجرای تاریخی و اطلاعات اجرای آیندهٔ پیش‌بینی‌شده، فازر می‌تواند به‌صورت هوشمند مسیر بهینه و امکان‌پذیر برای رسیدن به نقطهٔ هدف را تولید کند. با اجتناب از مسیرهای غیرقابل اجرا یا دشوار برای اجرا، فازر می‌تواند با دقت و کارایی بالاتری به نقطهٔ هدف دست یابد.

برای این منظور، ما DGF را به‌عنوان فرایندی برای رسیدن به نقطهٔ هدف از طریق توالی‌های مشخصی از انتقال مسیر مدل‌سازی می‌کنیم و این مدل را مدل انتقال مسیر (Path Transition Model) می‌نامیم. بذرهای جدیدی که از طریق جهش (Mutation) تولید می‌شوند، موجب ایجاد انتقال مسیر می‌گردند. ما از پاداش آنی (Immediate Reward) برای ارزیابی تأثیر مستقیم انتقال‌های مسیر بر عملکرد فازر استفاده می‌کنیم. همچنین، از پاداش توالی (Sequence Reward) برای سنجش میزان دشواری رسیدن به نقطهٔ هدف از طریق یک توالی از انتقال‌های مسیر بهره می‌بریم. مسیری که متناظر با یک توالی انتقال مسیر با پاداش بالا باشد، نشان‌دهندهٔ احتمال بالاتر رسیدن به نقطهٔ هدف از طریق آن مسیر است.

در مقایسه با روش‌های ابتکاری (Heuristic) پیشین، این مدل میزان دشواری رسیدن به نقطهٔ هدف از طریق توالی‌های مختلف انتقال مسیر را به‌طور صریح در نظر می‌گیرد. افزون بر این، با تحلیل پاداش‌های توالی مربوط به توالی‌های مختلف انتقال مسیر، می‌توان یک مسیر بهینه با بیشترین پاداش توالی را استخراج کرد که از آن برای هدایت مؤثرتر فازر به سمت نقطهٔ هدف استفاده می‌شود. برای دستیابی به این هدف، لازم است سه چالش اساسی مورد توجه و حل قرار گیرند.

چالش ۱: چگونه انتقال‌های مسیری را که تاکنون طی نشده‌اند پیش‌بینی کنیم؟
برای تولید مسیر بهینه به‌ سوی نقطهٔ هدف، لازم است تمامی انتقال‌های بالقوهٔ مسیر جمع‌آوری شوند. با این حال، تکنیک‌های موجود تنها قادر به گردآوری اطلاعات مربوط به انتقال‌های مسیر شناخته‌شده هستند و برای انتقال‌های مسیر آینده مناسب نیستند. در فازینگ هدایت‌شدهٔ خاکستری (DGF)، جهش‌های متفاوت منجر به انتقال‌های مسیر متفاوتی می‌شوند. با توجه به محدودیت بودجهٔ زمانی، فازر قادر نیست تمامی جهش‌های ممکن (برای مثال، استفاده از همهٔ جهش‌گرها بر روی تمام بایت‌های بذر) را بر روی بذرها امتحان کند. افزون بر این، انتخاب تصادفی جهش‌گرها و بایت‌ها برای جهش می‌تواند منجر به انتخاب جهش‌گرهای ناکارآمد و نادیده گرفتن بایت‌های کلیدی شود. بنابراین، لازم است انتقال‌های مسیر بالقوه و پاداش‌های متناظر با آن‌ها که ناشی از جهش‌هایی هستند که تاکنون اعمال نشده‌اند، پیش‌بینی شوند.

چالش ۲: چگونه مسیر بهینه را در میان تعداد زیادی از انتقال‌های مسیر تعیین کنیم؟
در مدل انتقال مسیر، پاداش توالی بالاتر نشان‌دهندهٔ احتمال بیشتر رسیدن به نقطهٔ هدف از طریق آن توالی انتقال مسیر است. مسیر بهینه را می‌توان به‌صورت یک توالی انتقال مسیر با بیشترین پاداش توالی نمایش داد. با این حال، ترکیب انتقال‌های مسیر تاریخی و انتقال‌های مسیر پیش‌بینی‌شده، تعداد بسیار زیادی از توالی‌های انتقال مسیر با پاداش‌های توالی متفاوت ایجاد می‌کند. ازاین‌رو، لازم است پاداش توالی تمامی توالی‌های انتقال مسیر به‌صورت کارآمد ارزیابی شود و یک سیاست مناسب طراحی گردد تا جهش‌ها را به‌گونه‌ای هدایت کند که مسیر بهینه محقق شود.

چالش ۳: چگونه با بهینه‌سازی راهبردهای فازینگ، توالی‌های انتقال مسیر بهینه را اجرا کنیم؟
از آن‌جا که DGF همچنان از راهبردهای جهش تصادفی استفاده می‌کند، مسیرهایی که توسط فازر پوشش داده می‌شوند تصادفی بوده و به‌ طور پیوسته تغییر می‌کنند. با این حال، بر اساس مدل انتقال مسیر، برای هدایت مؤثر فازر به‌سوی نقطهٔ هدف از طریق توالی انتقال مسیر بهینه، لازم است گام‌های کلیدی فازینگ به‌صورت جامع بهینه‌سازی شوند؛ از جمله انتخاب بذر، تخصیص انرژی، زمان‌بندی جهش‌گرها، چرخه‌های تکرار در مرحلهٔ havoc [83]، و انتخاب محل جهش. بنابراین، باید بتوان تمامی گام‌های بحرانی فازینگ را به‌طور هم‌زمان بهینه کرد تا توالی‌های انتقال مسیر بهینه به‌صورت کارآمد اجرا شوند.

برای مقابله با این چالش‌ها، ما DeepGo را به‌عنوان یک فازر خاکستری هدایت‌ شدهٔ پیش‌بینانه پیشنهاد می‌کنیم. بر پایهٔ مدل انتقال مسیر، در DGF مسیر پوشش‌ داده‌ شده توسط یک بذر، جهش اعمال‌ شده بر بذر، انتقال مسیر، و تغییرات مقدار بذر ناشی از انتقال مسیر را در قالب یک چهارتایی (path, action, next path, reward) استخراج می‌کنیم (رجوع شود به بخش 3).

برای چالش ۱، از شبکه‌های عصبی عمیق (DNNs) برای ساخت یک محیط ترکیبی مجازی (Virtual Ensemble Environment – VEE) استفاده می‌کنیم. با داشتن یک مسیر و یک عمل (Action)، VEE که به‌ خوبی آموزش دیده است می‌تواند انتقال‌های مسیر بالقوه و پاداش‌های متناظر با آن‌ها را پیش‌بینی کند. با افزایش تدریجی اطلاعات مربوط به انتقال‌های مسیر که به VEE ارائه می‌شود، این محیط می‌تواند به‌ تدریج مدل انتقال مسیر را تقلید کرده و انتقال‌های مسیری را که در اثر جهش‌های تاکنون اجرا نشده ایجاد می‌شوند، پیش‌بینی کند؛ امری که به‌طور چشمگیری کارایی DGF را افزایش می‌دهد.

برای چالش ۲، ما یک مدل یادگیری تقویتی برای فازینگ (Reinforcement Learning for Fuzzing – RLF) به‌منظور تعیین مسیر بهینه ارائه می‌دهیم. برای اعطای قابلیت پیش‌نگری به RLF، از یک راهبرد k-مرحله‌ای پیش‌روی شاخه (k-step branch rollout) استفاده می‌کنیم تا به‌طور پیوسته انتقال‌های مسیر پیش‌بینی‌شده را از VEE دریافت کنیم. با ترکیب انتقال‌های مسیر تاریخی و پیش‌بینی‌شده، مدل RLF آموزش داده می‌شود تا پاداش‌های توالی مورد انتظارِ توالی‌های انتقال مسیر ناشی از جهش‌های مختلف را ارزیابی کرده و بیشترین پاداش توالی را تعیین کند. افزون بر این، این مدل قادر است یک سیاست بهینه برای مسیر مطلوب بیاموزد تا راهبرد جهش در فرایند فازینگ را هدایت کند.

برای چالش ۳، به‌منظور اجرای مسیر بهینه، راهبردهای فازینگ را بر اساس مفهوم گروه عمل (Action Group) بهینه می‌کنیم. در گروه عمل، پنج گام حیاتی شامل انتخاب بذر، تخصیص انرژی، انتخاب تعداد چرخه‌های تکرار در مرحلهٔ havoc [83]، زمان‌بندی جهش‌گرها، و انتخاب محل جهش به‌صورت جامع در نظر گرفته می‌شوند. تحت سیاست جهشی که توسط مدل RLF تولید می‌شود، از الگوریتم بهینه‌سازی ازدحام ذرات چند عنصری (Multi-elements Particle Swarm Optimization – MPSO) برای بهینه‌سازی هم‌زمان این مؤلفه‌ها استفاده می‌کنیم تا جهش‌های مطلوب محقق شده، توالی‌های انتقال مسیر تولید گردند، و در نهایت از طریق مسیر بهینه به نقطهٔ هدف دست یابیم.

در مجموع، مهم‌ترین دستاوردهای این پژوهش به شرح زیر است:

مدل انتقال مسیر را ارائه می‌کنیم که در آن، DGF به‌عنوان فرایند رسیدن به نقطهٔ هدف از طریق توالی‌های مشخصی از انتقال مسیر مدل‌سازی می‌شود. بر پایهٔ این مدل، از پاداش توالی (Sequence Reward) به‌عنوان معیار برازندگی برای ارزیابی میزان دشواری رسیدن به نقطهٔ هدف از طریق یک توالی از انتقال‌های مسیر استفاده می‌کنیم.
محیط ترکیبی مجازی (VEE) را طراحی می‌کنیم که با بهره‌گیری از شبکه‌های عصبی عمیق (DNNs)، مدل انتقال مسیر را تقلید کرده و بدون اجرای واقعی مسیر، انتقال‌های مسیر بالقوه و پاداش‌های متناظر با آن‌ها را پیش‌بینی می‌کند؛ امری که به‌طور قابل‌توجهی کارایی سیستم را افزایش می‌دهد.
مدل یادگیری تقویتی برای فازینگ (RLF) را پیشنهاد می‌دهیم که قادر است با ترکیب اطلاعات تاریخی و اطلاعات پیش‌بینی‌شده، مسیر بهینه به‌سوی نقطهٔ هدف را تولید کند. با اجتناب از مسیرهای غیرقابل اجرا یا دشوار برای اجرا، مسیر بهینه با بیشترین پاداش توالی می‌تواند فازر را به‌صورت دقیق و کارآمد به نقطهٔ هدف هدایت کند.
راهبرد جهش در فرایند فازینگ را در سطح گروه عمل (Action Group) بهینه‌سازی می‌کنیم که نسبت به بهینه‌سازی تک‌راهبردی کاراتر است. در گروه عمل، پنج گام حیاتی فازینگ را به‌طور هم‌زمان و با استفاده از الگوریتم بهینه‌سازی ازدحام ذرات چند عنصری (MPSO یا Multi-elements Particle Swarm Optimization) بهینه می‌کنیم.
DeepGo را پیاده‌سازی و ارزیابی می‌کنیم. نتایج ارزیابی نشان می‌دهد که VEE قادر است انتقال‌های مسیر را با دقت بالا پیش‌بینی کند و DeepGo می‌تواند در مقایسه با فازرهای مبنا، سریع‌تر به نقاط هدف دست یابد.
پیاده‌سازی (Artifact) مربوط به DeepGo از طریق وب‌سایت ما در دسترس است: https://gitee.com/paynelin/DeepGo.

2. پیش‌زمینه (BACKGROUND)

2.1 فازینگ جعبه خاکستری هدایت‌شده (Directed Greybox Fuzzing)

مطابق با AFLGo [12]، روش‌های موجود DGF فاصله بین ورودی‌ها و اهداف از پیش تعریف‌شده را بر اساس گراف فراخوانی (Call Graph) و گراف جریان کنترل (Control-Flow Graph) محاسبه می‌کنند و این فاصله را با شاخص‌های دیگر (مانند پیچیدگی قیود شرطی) ترکیب می‌نمایند تا یک معیار برازندگی (Fitness Metric) شکل گیرد. سپس، در زمان اجرا، تکنیک‌های فازینگ خاکستری هدایت‌شده با توجه به این معیار برازندگی، زمان‌بندی‌های توان (Power Schedules) متفاوتی طراحی می‌کنند تا انرژی بیشتری به بذرهای ترجیح‌داده‌شده اختصاص یابد. در این رویکرد، مسئلهٔ قابلیت دسترسی به‌صورت یک مسئلهٔ بهینه‌سازی مدل‌سازی می‌شود که هدف آن کمینه‌سازی فاصله میان ورودی‌های تولیدشده و نقاط هدف است.

2.2 شبکه‌های عصبی عمیق (Deep Neural Networks):

در سال‌های اخیر، شبکه‌های عصبی عمیق (DNNs) توانایی خود را در تقریب توابع غیرخطی و غیرمحدب (non-linear and non-convex functions) پیچیده و نیز تقلید رفتار محیط در مسائل تشخیص الگو نشان داده‌اند [50]، [72]. DNNها در برخی از پژوهش‌های فازینگ، از جمله NEUZZ [69]، MTFuzz [68] و FUZZGUARD [93]، برای شبیه‌سازی رفتار شاخه‌بندی برنامه مورد استفاده قرار گرفته‌اند. به‌طور خلاصه، این پژوهش‌ها ورودی‌های جهش‌یافته‌ای را که در طول فرایند فازینگ تولید می‌شوند به‌عنوان ورودی DNNها جمع‌آوری کرده و شاخه‌های پوشش‌داده‌شدهٔ برنامه را به‌عنوان برچسب ثبت می‌کنند تا شبکه‌های عصبی آموزش داده شوند. بدین ترتیب، DNNها قادر خواهند بود رفتار شاخه‌بندی برنامه را شبیه‌سازی کرده و به بهینه‌سازی فرایند فازینگ کمک کنند. نتایج ارزیابی این مطالعات نشان می‌دهد که DNNها ابزار مناسبی برای شبیه‌سازی محیط فازینگ هستند.

2.3 یادگیری تقویتی (Reinforcement Learning)

یادگیری تقویتی (RL) [29]، [53]، [65] به‌طور گسترده برای حل مسائل تصمیم‌گیری دنباله‌ای (Sequential Decision Problems)، مانند فرایند مارکوف، مورد استفاده قرار می‌گیرد. در مدل RL، عامل‌ها (Agents) به‌ صورت پیوسته با انجام عمل‌ها با محیط تعامل می‌کنند و بازخوردی در قالب پاداش (Reward) دریافت می‌نمایند. بر اساس این بازخورد که به‌صورت یک چهارتایی (state, action, next state, reward) از محیط دریافت می‌شود، مدل RL راهبرد انتخاب عمل‌ها (یعنی سیاست در RL) را به‌گونه‌ای بهینه می‌کند که بیشترین پاداش ممکن حاصل شود.

با پیروی از AFLGo، می‌توان DGF را به‌عنوان یک فرایند مارکوف مدل‌سازی کرد و از مدل یادگیری تقویتی برای بهینه‌سازی راهبردهای فازینگ، از جمله انتخاب عملگرهای جهش و بایت‌های جهش، بهره گرفت.

2.4 بهینه‌سازی سیاست مبتنی بر مدل (Model-Based Policy Optimization – MBPO) [32]

MBPO یک روش یادگیری تقویتی مبتنی بر مدل است که از دو ماژول اصلی تشکیل می‌شود: یک محیط مجازی و یک شبکهٔ یادگیری تقویتی. در گام نخست، MBPO با استفاده از شبکه‌های عصبی عمیق (DNNs) یک محیط مجازی ایجاد می‌کند تا جایگزین محیط واقعی شود. در گام دوم، MBPO به عامل اجازه می‌دهد با این محیط مجازی تعامل داشته باشد و تعداد زیادی انتقال مسیر به‌دست آورد. سپس، MBPO با تکیه بر این انتقال‌های مسیر، شبکهٔ یادگیری تقویتی را به‌صورت پیوسته آموزش می‌دهد و سیاستی را می‌آموزد که پاداش عامل را بیشینه می‌کند.

در این مقاله، از برخی مفاهیم و روش‌های MBPO، از جمله راهبرد k-مرحله‌ای پیش‌روی شاخه (k-step branch rollout)، برای ترکیب شبکه‌های عصبی عمیق و یادگیری تقویتی استفاده می‌کنیم.

2.5 بهینه‌سازی ازدحام ذرات (Particle Swarm Optimization – PSO)

الگوریتم PSO [34] یک تکنیک محاسبات تکاملی است که از مطالعهٔ رفتار گروهی پرندگان هنگام جستجوی غذا الهام گرفته شده است. این الگوریتم برای افزایش کارایی فازینگ در CGF نیز به‌کار رفته است؛ برای مثال، MOPT [48] از الگوریتم PSO برای بهینه‌سازی احتمال انتخاب عملگرهای جهش بر اساس اطلاعات تاریخی فازینگ استفاده می‌کند.

ایدهٔ اصلی PSO یافتن راه‌حل بهینه از طریق همکاری و به‌اشتراک‌گذاری اطلاعات بین اعضای جمعیت است. الگوریتم PSO از ذرات بدون جرم برای شبیه‌سازی پرندگان در یک گروه استفاده می‌کند، و هر ذره دو ویژگی اصلی دارد: سرعت (Velocity) و مکان (Position). سرعت نشان‌دهندهٔ میزان حرکت و مکان نشان‌دهندهٔ جهت حرکت ذره است. هر ذره به‌صورت مستقل در فضای جستجو به دنبال راه‌حل بهینه می‌گردد و آن را به‌عنوان بهترین مقدار محلی (Local Best) ثبت می‌کند. سپس بهترین مقادیر محلی بین تمامی ذرات جمعیت به اشتراک گذاشته می‌شود تا بهترین مقدار کلی (Global Best) به‌ عنوان راه‌حل بهینه تعیین گردد. تمامی ذرات موجود در جمعیت بر اساس مقدار بهترین محلی و بهترین مقدار کلی به‌اشتراک گذاشته‌شده، سرعت و مکان خود را تنظیم می‌کنند.

3. مدل انتقال مسیر (PATH TRANSITION MODEL)

در این مقاله، ما مدل انتقال مسیر را پیشنهاد می‌کنیم که در آن، DGF به‌ عنوان فرایندی برای رسیدن به نقطهٔ هدف از طریق توالی‌های مشخصی از انتقال مسیر مدل‌سازی می‌شود. بذرهای جدیدی که از طریق جهش تولید می‌شوند، موجب انتقال مسیر می‌گردند و ما از پاداش‌ها (Rewards) برای ارزیابی تأثیر فوری این انتقال‌های مسیر بر فازر استفاده می‌کنیم. توالی انتقال مسیری که دارای بیشترین پاداش توالی (Sequence Reward) باشد، مسیر بهینه به نقطهٔ هدف را تعیین می‌کند.

در این بخش، عناصر کلیدی موجود در DGF را به مدل انتقال مسیر نگاشت می‌کنیم و اثربخشی انتقال‌های مسیر و اقدامات (Actions) را کمّی‌سازی می‌نماییم.

3.1 عناصر مدل انتقال مسیر (Elements in Path Transition Model):

مسیر (Path). هر مسیر متناظر با یک بذر در صف بذرهای فازر است. ما از trace_bits در AFL [12] برای ثبت شاخه‌های پوشش‌داده‌شده و تعداد برخوردهای هر شاخه در مسیر استفاده می‌کنیم و مسیرهای مختلف را متمایز می‌نماییم.
اقدام (Action). اقدام یک فازر به معنای جهش یک بذر در مکان مشخصی است. تمرکز ما بر محل جهش (بایت‌ها) است و نه جهش‌گر مورد استفاده. فازر با انجام یک سری اقدامات، به‌صورت تدریجی به نقطهٔ هدف نزدیک می‌شود.
انتقال مسیر (Path Transition). جهش روی بذر موجب انتقال مسیر می‌شود اگر مسیر اجرای ورودی جدید با مسیر بذر متفاوت باشد. اگر مسیر ورودی جدید با مسیر بذر یکسان باشد، جهش یک انتقال مسیر خودی (Self-Path-Transition) ایجاد می‌کند.
پاداش (Reward). پاداش یک انتقال مسیر نشان‌دهندهٔ تغییر در ارزش بذر است که ناشی از آن انتقال مسیر می‌باشد.
سیاست (Policy). سیاست، راهبرد انتخاب عمل‌ها توسط فازر در هر مسیر است و به‌صورت یک فهرست از احتمال‌ها متناظر با هر عمل نمایش داده می‌شود. تحت این سیاست، فازر عمل‌ها را با احتمال‌های متفاوت انتخاب می‌کند.

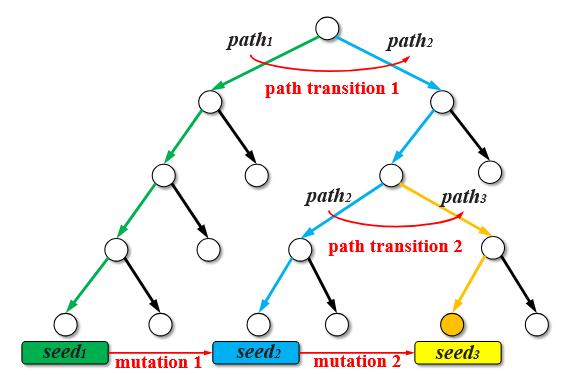
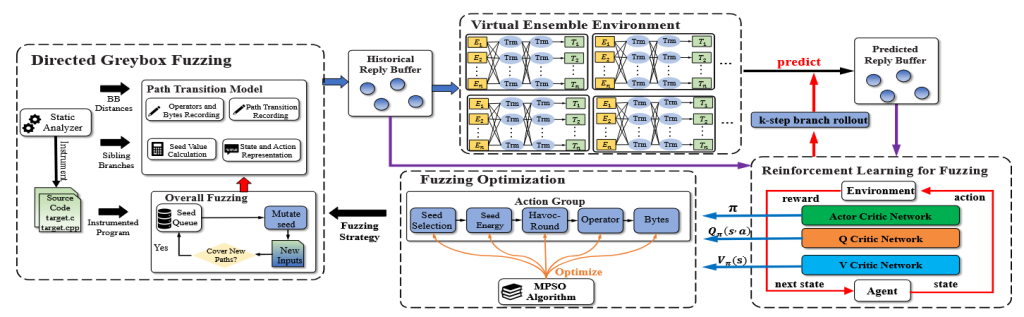
ما از شکل ۱ برای نمایش مدل انتقال مسیر استفاده می‌کنیم. شکل ۱ درخت اجرای یک برنامه نمونه را نشان می‌دهد که در آن، گره‌ها نمایانگر بلاک‌های پایه (Basic Blocks) و یال‌ها نمایانگر انتقال بین بلاک‌های پایه هستند. مسیر اجرای path1 که با رنگ سبز مشخص شده، توسط بذر s1 پوشش داده می‌شود؛ مسیر path2 با رنگ آبی توسط بذر s2 پوشش داده شده و مسیر path3 با رنگ زرد توسط بذر s3 پوشش داده می‌شود. گره‌ای که با رنگ نارنجی مشخص شده، بلاک پایه هدف (Target Basic Block) است و مسیر path3 مسیر بهینه‌ای است که می‌تواند به نقطهٔ هدف برسد.

در طول فرایند فازینگ، ابتدا فازر با اقدام به جهش بذر s1، بذر جدید s2 را تولید می‌کند و مسیر path1 به path2 منتقل می‌شود. سپس فازر با اقدام به جهش بذر s2، مسیر path2 را به path3 منتقل می‌کند و به نقطهٔ هدف دست می‌یابد. از طریق این دو انتقال مسیر، فازر مسیر بهینه path3 را تولید می‌کند که توسط یک توالی انتقال مسیر (Path Transition Sequence) شامل انتقال مسیر ۱ و انتقال مسیر ۲ نمایش داده شده و به نقطهٔ هدف منتهی می‌شود.

3.2 کمّی‌سازی انتقال‌های مسیر و اقدامات (Quantifying Path Transitions and Actions):

فازر با انجام اقدامات مختلف برای جهش بذرها، باعث ایجاد انتقال‌های مسیر متفاوت می‌شود. ما از پاداش‌ها (Rewards) برای کمّی‌سازی اثربخشی انتقال‌های مسیر استفاده می‌کنیم و از پاداش توالی مورد انتظار (Expected Sequence Rewards) برای کمّی‌سازی اثربخشی اقدامات (Actions) بهره می‌بریم.

مقدار بذر (Seed Value). ما از مقدار بذر برای ارزیابی مسیرهای مختلف استفاده می‌کنیم تا میزان سهم آن‌ها در رسیدن فازر به نقطهٔ هدف مشخص شود. مقدار بذر بر اساس چهار ویژگی بذر متناظر با مسیر محاسبه می‌شود:

فاصله بذر تا هدف (Seed Distance to the Target)
دشواری برآورده کردن معکوس شاخه (Difficulty of Satisfying Branch Inversion)
سرعت اجرای بذر (Execution Speed)
آیا بذر «ترجیح داده شده» است یا خیر (Favored Seed)

در DGF، فاصله کوتاه‌تر بذر نشان می‌دهد که فازر می‌تواند با برآورده کردن تعداد کمتری از قیود مسیر، به نقطهٔ هدف برسد و دشواری کمتر نشان‌دهندهٔ آسان‌تر بودن برآورده کردن قیود مسیر منتهی به نقطهٔ هدف است. علاوه بر این، در طول اجرای بذر، فازر ممکن است در حلقه‌ها (مثلاً while و for) گرفتار شود که این امر سرعت اجرا را کاهش داده و کمکی به رسیدن به نقطهٔ هدف نمی‌کند. بنابراین، برای افزایش کارایی فازینگ، بذرهایی که سرعت اجرای بالاتری دارند ترجیح داده می‌شوند.

همچنین، بذرهایی که به‌عنوان «ترجیح داده شده» (Favored) علامت‌گذاری شده‌اند، ترجیح داده می‌شوند زیرا این بذرها می‌توانند تمام شاخه‌های کاوش‌ شده را پوشش دهند. با فازینگ بذرهای ترجیح داده شده، می‌توان معکوس شاخه (Branch Inversion) را روی همهٔ شاخه‌های کاوش‌شده انجام داد تا شاخه‌های جدید منتهی به نقطهٔ هدف پوشش داده شوند.

مطابق با روش‌های AFL [39] و AFLGo [12]، عناصر (1)، (3) و (4) می‌توانند با ثبت اطلاعات اجرا در طول فازینگ به‌دست آیند. در اینجا، تمرکز ما بر توضیح مفهوم «دشواری» (Difficulty) و روش محاسبهٔ آن است.

ما از احتمال شاخه (Branch Probability) برای سنجش دشواری برآورده کردن معکوس شاخه (Branch Inversion) استفاده می‌کنیم، که بر پایهٔ آمار برخوردهای شاخه (Branch Hits) محاسبه می‌شود. ابتدا، اطلاعات مربوط به شاخه‌های هم‌سطح (Sibling Branches) هر شاخه را طی تحلیل ایستا (Static Analysis) به‌دست می‌آوریم. اگر شاخه‌های هم‌سطح شاخه‌های پوشش داده‌شده هنوز پوشش داده نشده باشند (یعنی شاخه‌های کاوش‌ نشده)، برآورده کردن معکوس شاخه برای پوشش این شاخه‌های کاوش‌نشده، فازر را قادر می‌سازد تا از مسیرهای پوشش داده‌شده به مسیرهای جدید منتقل شود.

سپس، تعداد برخوردهای شاخه را می‌شماریم تا احتمال شاخه (Branch Probability) شاخهٔ کاوش‌ نشده را محاسبه کنیم. اگر فازر به‌طور مداوم با ورودی‌های جهش‌یافته به شاخه‌های پوشش داده‌شده برخورد کند اما نتواند به شاخه‌های کاوش‌نشده برسد، این امر نشان‌دهندهٔ مشکل فازر در برآورده کردن معکوس شاخه است.

در نهایت، دشواری برآورده کردن معکوس شاخه را از طریق احتمال شاخه کمّی می‌کنیم:

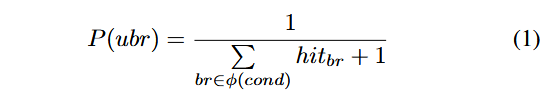
که در آن، ubr شاخه‌ای کاوش‌ نشده را نشان می‌دهد. برای یافتن شاخه‌های کاوش‌نشده، بررسی می‌کنیم که آیا شاخه‌های هم‌سطح شاخه‌های پوشش داده‌شده پوشش داده شده‌اند یا خیر. ϕ(cond) مجموعهٔ تمامی شاخه‌ها تحت همان شرط (Condition) را نشان می‌دهد. hitbr تعداد برخوردهای شاخه‌ای است که در طول فازینگ ثبت شده است. P(ubr) احتمال شاخهٔ شاخه‌های کاوش‌نشده را نشان می‌دهد، که هرگز برابر با صفر نیست، زیرا فرض ما این است که شاخه‌های کاوش‌نشده همواره احتمال پوشش توسط فازینگ را دارند.

به منظور برآورد دشواری برآورده کردن معکوس شاخه، از میانگین حسابی احتمالات شاخهٔ تمام شاخه‌های کاوش‌نشده در مسیر یک بذر استفاده می‌کنیم:

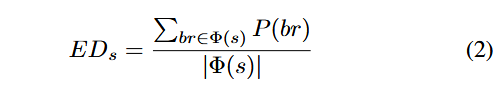
که در آن، s بذر را نشان می‌دهد، EDs دشواری تخمینی (Estimated Difficulty) را نشان می‌دهد و Φ(s) مجموعه‌ای از تمامی شاخه‌های کاوش‌نشده در مسیر بذر است. بنابراین، فاصله (Distance)، دشواری (Difficulty)، سرعت اجرا (Execution Speed) و ترجیح داده شدن (Favored) همگی می‌توانند به‌صورت کمّی اندازه‌گیری و محاسبه شوند تا مقدار بذر (Seed Value) تعیین گردد.

ما از روش وزن‌دهی بر پایه آنتروپی (Entropy Weight Method) [42] برای تعیین وزن‌های چهار عامل استفاده می‌کنیم، که بر اساس آنتروپی اطلاعاتی هر عامل محاسبه می‌شود. مقدار کوچک آنتروپی اطلاعاتی، وزن کوچک برای آن عامل ایجاد می‌کند و نشان می‌دهد که تأثیر آن عامل بر ارزیابی کلی مقدار بذر کم است.

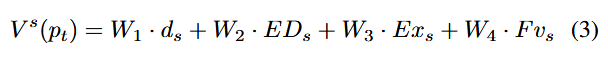
که در آن، Vs(pt) مقدار بذر مسیر pt را نشان می‌دهد، و W1, W2, W3, W4 وزن‌هایی هستند که بر اساس روش وزن‌دهی آنتروپی (Entropy Weight Method) محاسبه شده‌اند. ds فاصله بذر، Exs سرعت اجرای بذر و Fvs نشان‌دهندهٔ وضعیت ترجیح داده شدن بذر است که مقدار آن می‌تواند ۰ یا ۱ باشد. روش وزن‌دهی آنتروپی [42] یک روش رایج برای ارزیابی جامع چندعنصری (Multi-Element Comprehensive Evaluation) است. مراحل محاسبهٔ وزن‌های عناصر مختلف به شرح زیر است:

(1) محاسبهٔ آنتروپی هر عنصر (Calculate the Entropy of Each Element):

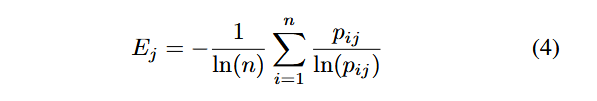
(2) محاسبهٔ وزن هر عنصر (Calculate the Weight of Each Element):

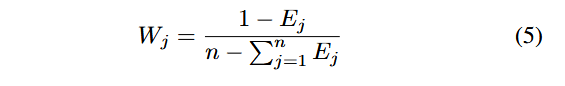
(3) نرمال‌سازی وزن هر عنصر (Normalize the Weight of Each Element):

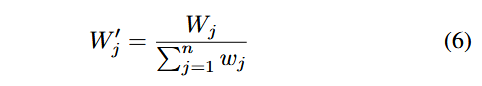
که در آن، W′j وزن نرمال‌شدهٔ عنصر jام را نشان می‌دهد. ایدهٔ اصلی روش وزن‌دهی آنتروپی این است که با محاسبهٔ آنتروپی هر عنصر، وزن آن تعیین شود تا بتوان ارزیابی جامع چندعنصری انجام داد. سپس، با استفاده از مقدار بذر (Seed Value)، پاداش (Reward) محاسبه می‌شود تا اثربخشی انتقال مسیر (Effectiveness of the Path Transition) ارزیابی گردد.

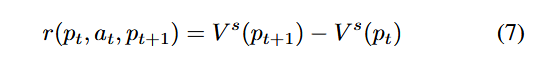
که در آن، r(pt, at, pt+1) پاداش را نشان می‌دهد، at عملی است که فازر برای انتقال از مسیر pt به مسیر pt+1 انجام می‌دهد، و Vs(pt+1) و Vs(pt) مقدار بذر مسیرهای pt+1 و pt را نشان می‌دهند. ما از چهارتایی (pt, at, pt+1, rt) برای نمایش یک انتقال مسیر (Path Transition) استفاده می‌کنیم.

پاداش توالی مورد انتظار (Expected Sequence Reward). در مدل انتقال مسیر، انتقال‌های مسیر که ناشی از انتخاب عمل‌ها بر اساس سیاست (Policy) هستند، بر توالی‌های بعدی انتقال مسیر تأثیر می‌گذارند و بنابراین بر رسیدن به نقطهٔ هدف اثر می‌گذارند. برای ارزیابی سهم انتقال‌های مسیر در رسیدن به نقطهٔ هدف، ما پاداش توالی مورد انتظار را به‌عنوان مجموع مورد انتظار پاداش‌های توالی‌های انتقال مسیر که توسط فازر تحت یک سیاست مشخص تولید می‌شوند، تعریف می‌کنیم. این مقدار را می‌توان به‌صورت بازگشتی با استفاده از معادلهٔ بلمن (Bellman Equation) [7] محاسبه کرد:

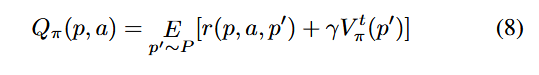
که در آن، p′ ∼ P نشان‌دهندهٔ احتمال انتقال از مسیر p به مسیر ′p است. γ عامل تنزیل (Discount Factor) را نشان می‌دهد و تأثیر انتقال‌های مسیر بعدی بر پاداش توالی مورد انتظار به‌تدریج کاهش می‌یابد. r(p, a, p′) پاداش انتقال مسیر را نشان می‌دهد و Vtπ(p′) مقدار انتقال مسیر ′p است.

محاسبهٔ مقدار انتقال مسیر ′p به صورت زیر انجام می‌شود:

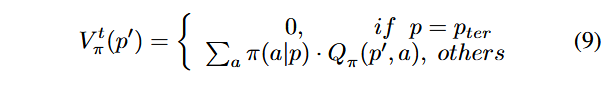
که در آن، pter مسیر پایانی (Terminal Path) را نشان می‌دهد. مسیری را پایانی در نظر می‌گیریم که تمام اقدامات آن مسیر تنها موجب انتقال مسیر خودی (Self-Path-Transition) شوند. π نشان‌دهندهٔ سیاست (Policy) برای انتخاب اقدامات است (برای مثال، در AFL، فازر از سیاست تصادفی (Random Policy) برای انتخاب اقدامات جهش استفاده می‌کند). π(a|p) احتمال انتخاب عمل a توسط مسیر p تحت سیاست π را نشان می‌دهد.

اگر ′p وضعیت پایانی باشد، مقدار انتقال آن برابر با صفر است. در غیر این صورت، مقدار انتقال آن برابر با میانگین وزنی پاداش‌های توالی مورد انتظار تمام اقدامات است. معادلهٔ بلمن (Bellman Equation) برای به‌روزرسانی بازگشتی مقدار انتقال و پاداش توالی مورد انتظار استفاده می‌شود تا مسیر به مسیر پایانی برسد. با بیشینه کردن پاداش توالی مورد انتظار (Expected Sequence Reward)، فازر می‌تواند سیاستی بیاموزد که پاداش تجمعی بلندمدت (Long-Term Cumulative Reward) را به حداکثر برساند.

4. روش (METHOD)

4.1 نمای کلی DeepGo

بر پایهٔ مدل انتقال مسیر، ما یک فازر خاکستری هدایت‌شدهٔ پیش‌بینانه (Predictable Directed Greybox Fuzzer) با نام DeepGo طراحی کرده‌ایم. DeepGo از شبکه‌های عصبی عمیق (DNNs) برای پیش‌بینی انتقال‌های مسیر بالقوه و پاداش‌های متناظر استفاده می‌کند. سپس با بهره‌گیری از یادگیری تقویتی (Reinforcement Learning)، انتقال‌های مسیر تاریخی و پیش‌بینی‌ شده را ترکیب می‌کند تا توالی انتقال مسیر بهینه همراه با سیاست متناظر (Policy) آن به‌دست آید.

در نهایت، بر اساس گروه عمل (Action Group)، راهبردهای فازینگ به‌ صورت جامع بهینه‌سازی می‌شوند تا توالی‌های انتقال مسیر بهینه به‌طور مؤثر اجرا شوند. همان‌طور که در شکل ۲ نشان داده شده است، DeepGo عمدتاً از چهار جزء اصلی تشکیل شده است.

4.1.1 مولفه فازینگ خاکستری هدایت‌ شده (Directed Greybox Fuzzing Component)

مولفه DGF به‌صورت مداوم بذرها را جهش می‌دهد تا ورودی‌هایی برای رسیدن به نقاط هدف تولید کند. این جزء شامل یک تحلیل‌گر ایستا (Static Analyzer) و یک فازر (Fuzzer) است. در زمان کامپایل، تحلیل‌گر ایستا فاصله در سطح بلاک پایه (BB Distance) را محاسبه می‌کند، شاخه‌های هم‌سطح هر شاخه را ثبت می‌کند و برنامهٔ هدف را ابزارسنجی (Instrument) می‌نماید. پس از راه‌اندازی کمپین فازینگ، فازر به‌طور مداوم بذرها را جهش داده و برنامه را تست می‌کند. لازم به ذکر است که مدل انتقال مسیر در جزء DGF ادغام شده است.

4.1.2 محیط ترکیبی مجازی (Virtual Ensemble Environment – VEE)

VEE برای پیش‌بینی انتقال‌های مسیر بالقوه و پاداش‌های متناظر استفاده می‌شود. VEE شامل شبکه‌های عصبی عمیق (DNNs) است و با جزء یادگیری تقویتی برای فازینگ (Reinforcement Learning for Fuzzing)، بافر بازپخش تاریخی (Historical Replay Buffer) و بافر بازپخش پیش‌بینی‌شده (Predicted Replay Buffer) را به اشتراک می‌گذارد. این دو بافر داده‌ای، شامل چهارتایی‌ها (Four-Tuples) یعنی (Path, Action, Next Path, Reward) هستند. با داشتن یک چهارتایی (Path, Action)، VEE آموزش‌دیده مسیر بعدی و پاداش اقدام را، مطابق با احتمال‌های مختلف انتقال مسیر، پیش‌بینی می‌کند و آن را به‌صورت (Next Path, Reward) نمایش می‌دهد.

4.1.3 مدل یادگیری تقویتی برای فازینگ (Reinforcement Learning for Fuzzing – RLF)

این مدل از یادگیری تقویتی استفاده می‌کند تا انتقال‌های مسیر تاریخی و پیش‌بینی‌شده را ترکیب کرده و سیاستی (Policy) بیاموزد که پاداش‌های توالی (Sequence Rewards) را بیشینه کند. مدل RLF شامل سه شبکه اصلی است:

شبکه Actor
شبکه Q-Critic
شبکه V-Critic

پس از آموزش:

شبکه Q-Critic می‌تواند پاداش توالی مورد انتظار Qπ(p, a) ناشی از هر عمل را ارزیابی کند.
شبکه V-Critic می‌تواند مقدار انتقال مسیر Vtπ(p) هر مسیر را ارزیابی نماید.
شبکه Actor می‌تواند سیاست π را بیاموزد تا پاداش‌های توالی را به حداکثر برساند.

4.1.4 مولفه بهینه‌سازی فازینگ (Fuzzing Optimization Component)

این مولفه توالی‌های انتقال مسیر بهینه را با بهینه‌سازی راهبردهای فازینگ اجرا می‌کند. بر اساس گروه عمل (Action Group)، می‌توان گام‌های حیاتی فازینگ را به‌صورت جامع بهینه کرد و برای این منظور از الگوریتم بهینه‌سازی ازدحام ذرات چندعنصری (Multi-elements Particle Swarm Optimization – MPSO) استفاده می‌شود تا عناصر یک گروه عمل به‌طور هم‌زمان بهینه شوند.

ما فرایند فازینگ DeepGo را به چرخه‌های فازینگ (Fuzzing Cycles) تقسیم می‌کنیم که هر چرخه تقریباً ۲۰ دقیقه طول می‌کشد. در هر چرخهٔ فازینگ، DeepGo باید چهار کار زیر را انجام دهد:

استفاده از فازر برای تست برنامه‌ها و ارائه انتقال‌های مسیر تاریخی به منظور آموزش VEE و مدل
VEE ارائهٔ انتقال‌های مسیر پیش‌بینی‌شده به منظور آموزش مدل
RLF ارائهٔ مقدار انتقال‌ها، پاداش‌های توالی مورد انتظار، و سیاست (Policy) به جزء
جزء FO با استفاده از الگوریتم MPSO، گروه عمل را بهینه کرده و راهبردهای بهینه فازینگ را به DGF ارائه می‌دهد.

پس از انجام این چهار کار، DeepGo وارد چرخهٔ بعدی فازینگ می‌شود و این چهار کار را تکرار می‌کند.

4.2 محیط ترکیبی مجازی (Virtual Ensemble Environment)

برای طراحی سیاستی (Policy) که بتواند فازر را به مسیرهای بهینه هدایت کند، فازر باید پاداش تمام انتقال‌های مسیر ناشی از اقدامات انجام‌شده در مسیرها را به‌دست آورد. با این حال، فازر نمی‌تواند تمام اقدامات را در همه مسیرها در بودجهٔ زمانی محدود (مثلاً ۲۴ ساعت) انجام دهد.

برای پیش‌بینی انتقال‌های مسیر بالقوه و پاداش‌های متناظر ناشی از اقداماتی که هنوز انجام نشده‌اند، ما VEE را طراحی کرده‌ایم تا مدل انتقال مسیر را تقلید کند و انتقال‌های مسیر بالقوه و پاداش‌های متناظر آن‌ها را پیش‌بینی نماید.

4.2.1 رمزگذاری ورودی و خروجی (Input and Output Encoding):

قبل از آموزش VEE، باید مسیر (Path)، عمل (Action) و پاداش (Reward) را رمزگذاری کنیم. ما روش رمزگذاری VEE را با دو هدف طراحی کرده‌ایم. نخست آن که VEE بتواند انتقال‌های مسیر بالقوه برای مسیرهای جدید را بر اساس انتقال‌های مسیر ثبت‌شده در مسیرهای کاوش‌شده پیش‌بینی کند و دلیل دوم، برای بهبود کارایی آموزش VEE، لازم است از بردارهای با بعد پایین (Low-Dimensional Vectors) برای نمایش مسیرها و اقدامات استفاده کنیم. برای مثال، نگاشت trace_bits به یک بردار ۶۵۵۳۶ بعدی برای نمایش مسیر، به‌طور قابل توجهی سرعت آموزش شبکه‌های عصبی عمیق (DNNs) را کاهش می‌دهد. بنابراین، در حالی که اطمینان حاصل می‌کنیم که مسیرها و اقدامات مختلف به‌وضوح قابل تمایز باشند، سعی می‌کنیم از بردارهای با بعد پایین برای نمایش مسیرها، اقدامات و پاداش‌ها استفاده کنیم.

مسیر (Path). ما از الگوریتم Coupled Data Embedding (CDE) [33]برای رمزگذاری مسیرها (نمایش داده‌شده توسط trace_bits در AFL) به بردارهای پیوسته ۲۰ بعدی (20-Dimensional Continuous Vectors) استفاده می‌کنیم و مقادیر هر بعد را نرمال‌سازی می‌کنیم. CDE برای نمایش بردارهای گسسته به صورت بردارهای پیوسته به‌کار می‌رود و در عین حال ویژگی‌های اصلی که مسیرها را متمایز می‌کنند حفظ می‌شوند. بر اساس روش CDE، یک بردار ۲۰ بعدی می‌تواند ویژگی‌های اصلی مسیرهای مختلف را متمایز کند و همزمان بعد مسیرها را کاهش دهد تا کارایی آموزش شبکه‌های عصبی عمیق (DNNs) افزایش یابد. اگر دو مسیر نمایش داده‌شده با trace_bits به یکدیگر شباهت بیشتری داشته باشند، فاصله اقلیدسی (Euclidean Distance) بین بردارهای ۲۰ بعدی متناظر آن‌ها کمتر خواهد بود.

عمل (Action). ما عمل را بر اساس مکان جهش (Mutation Location) رمزگذاری می‌کنیم. به مثال شکل ۱ توجه کنید: بذر s1 شامل ۱۰۰ بایت است. اگر فازر بایت چهارم از s1 را به‌عنوان مکان جهش انتخاب کند، صرف‌نظر از اینکه کدام جهش‌گر (Mutator) انتخاب شود، فازر از بایت چهارم s1 را جهش می‌دهد. رمزگذاری این عمل برابر است با: 4/100=0.04. مقادیر تمام اعمال (Actions) نیز نرمال‌سازی می‌شوند.

پاداش (Reward). پاداش یک مقدار اسکالر است که مطابق معادلهٔ۷ محاسبه می‌شود. استفاده از این روش رمزگذاری به VEE امکان می‌دهد تا احتمال و پاداش انتقال‌های مسیر بالقوه را بر اساس اطلاعات تاریخی فازینگ پیش‌بینی کند.

VEE با استفاده از چهارتایی‌ها (Four-Tuples) آموزش داده می‌شود (path,action,next path,reward) که در آن، action نشان‌دهندهٔ بایت‌های یک بذر است که جهش می‌توانند در آن‌ها رخ دهند و نه یک جهش مشخص. بنابراین، یک عمل مشابه با جهش‌گرهای مختلف می‌تواند انتقال‌های مسیر متفاوت با احتمال‌های مختلف ایجاد کند.

با تحلیل اطلاعات تاریخی جهش‌ها روی یک بایت، VEE می‌تواند انتقال‌های مسیر ناشی از انجام این عمل را پیش‌بینی کند، یعنی جهش آن بایت با جهش‌گرهای مختلف.

برای بایت‌هایی که قبلاً جهش داده شده‌اند، از VEE برای پیش‌بینی احتمال‌ها و پاداش‌های انتقال مسیرهای مختلف ناشی از جهش آن بایت با جهش‌گرهای مختلف استفاده می‌کنیم.
برای بذرها یا بایت‌هایی که هنوز جهش داده نشده‌اند، از بذرهای با ساختار مشابه یا بایت‌هایی با افست مشابه برای پیش‌بینی احتمال‌ها و پاداش‌های انتقال مسیر ناشی از اقدامات جهش استفاده می‌کنیم.

شباهت بر اساس روش رمزگذاری CDE سنجیده می‌شود. اگر بردارهای ۲۰ بعدی که دو بذر را نمایش می‌دهند، فاصلهٔ اقلیدسی کوتاه‌تری داشته باشند، نشان‌دهندهٔ این است که دو بذر شباهت بیشتری دارند.

علاوه بر این، در داخل یک بذر، مقادیر رمزگذاری‌ شده مشابه دو عمل نشان‌دهندهٔ افست مشابه بایت‌های متناظر است.

4.2.2 آموزش VEE (Training of VEE)

ما از شبکه‌های عصبی عمیق (DNNs) برای ساخت VEE استفاده می‌کنیم تا رفتار انتقال مسیر در مدل انتقال مسیر را شبیه‌سازی کند. به‌طور رسمی، فرض کنید:

f:(path, action) → (next path, reward) نمایانگر شبکه‌های عصبی (DNNs) است که چهارتایی (path, action) را به‌عنوان ورودی دریافت کرده و چهارتایی (next path, reward) را به‌عنوان خروجی تولید می‌کند.

ما از θ برای نمایش پارامترهای قابل آموزش DNN استفاده می‌کنیم و شبکه را با مجموعه‌ای از نمونه‌های آموزشی (X, Y) آموزش می‌دهیم، که در آن X مجموعه ورودی‌ها و Y خروجی‌های متناظر آن‌ها است.

در مدل انتقال مسیر، از آنجا که یک عمل مشابه روی یک مسیر مشابه ممکن است باعث انتقال‌های مسیر متفاوت با احتمال‌های مختلف شود، مدل انتقال مسیر ذاتاً یک مدل احتمالاتی (Probabilistic Model) است. بنابراین، هنگام طراحی DNN به شکل f:(path, action) → (next path, reward) است و تابع خطا (Loss Function)، ما به‌ویژه به نااطمینانی‌های آلیاتوریک (Aleatoric) و اپیستمیک (Epistemic) VEE توجه می‌کنیم تا دقت پیش‌بینی آن بهبود یابد.

نااطمینانی آلیاتوریک (Aleatoric Uncertainty). نااطمینانی آلیاتوریک (به نااطمینانی ناشی از ذاتی فرآیند یا داده‌ها اشاره دارد، یعنی چیزی که به دلیل طبیعت تصادفی سیستم وجود دارد و قابل حذف نیست) ناشی از غیرقابل پیش‌بینی بودن انتقال‌های مسیر در فازینگ است. به عنوان مثال، استفاده از جهش‌گرهای مختلف برای یک مکان جهش مشابه می‌تواند منجر به انتقال‌های مسیر متفاوت شود.

برای مدل‌سازی نااطمینانی آلیاتوریک، ما از توزیع احتمال گاوسی (Gaussian Probability Distribution) برای مسیرهای بعدی و پاداش‌ها استفاده می‌کنیم تا احتمال‌های انتقال مسیرهای مختلف و پاداش‌های متناظر که ممکن است توسط عمل at در مسیر pt ایجاد شوند، پیش‌بینی شود.

ما از پارامترهای قابل آموزش (Trainable Weight Parameters) برای نمایش توزیع گاوسی مسیر بعدی pt+1 و پاداش rt استفاده می‌کنیم که می‌تواند براساس چهارتایی ورودی (pt, at) نمایش داده شود:

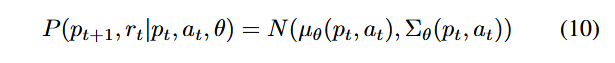
که در آن، N نمایانگر توزیع گاوسی (Gaussian Distribution) است و μθ میانگین توزیع گاوسی را نشان می‌دهد. ما از Σθ برای نمایش واریانس استفاده می‌کنیم که نشان‌دهندهٔ نااطمینانی نسبت به میانگین است. تابع خطا (Loss Function) بین خروجی شبکه عصبی عمیق (DNN) و برچسب واقعی y ∈ Y در مجموعه آموزش به صورت زیر تعریف می‌شود:

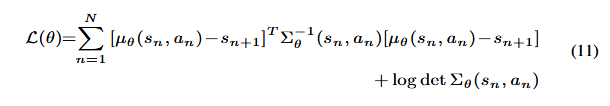
وظیفهٔ آموزش (Training Task) این است که پارامترهای وزنی θˆ شبکه عصبی f را پیدا کنیم تا تابع خطا (Loss) به حداقل برسد.

نااطمینانی اپیستمیک (Epistemic Uncertainty). نااطمینانی اپیستمیک ناشی از روش نمونه‌گیری تصادفی است که در اکثر شبکه‌های عصبی عمیق (DNNs) به‌کار می‌رود. از آنجا که یک DNN واحد نمی‌تواند تمام داده‌های آموزشی را نمونه‌برداری کند، ممکن است ناحیه‌هایی وجود داشته باشند که DNN در آن‌ها نقص شناختی (Epistemic Defect) دارد و قادر به پیش‌بینی دقیق خروجی‌ها نیست.

برای مدل‌سازی نااطمینانی اپیستمیک، ما از الگوریتم Probabilistic Ensembles with Trajectory Sampling (PETS) [21] استفاده کردیم تا تمام DNNها را در یک محیط ترکیبی مجازی (Virtual Ensemble Environment) جمع‌آوری کنیم.

ما از همان روش نمونه‌گیری تصادفی برای آموزش DNNها استفاده می‌کنیم، به طوری که چهارتایی‌ها (Four-Tuples) از بافر بازپخش تاریخی (Historical Replay Buffer) نمونه‌برداری شوند.

تمام DNNها خروجی‌های پیش‌بینی‌ شده را به صورت توزیع‌های احتمال گاوسی (Gaussian Probability Distributions) تولید می‌کنند و نتایج آن‌ها با وزن‌دهی ترکیب شده تا یک پیش‌بینی نهایی حاصل شود. این پیش‌بینی را می‌توان به صورت زیر توصیف کرد:

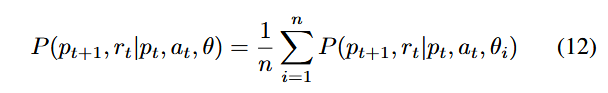
که در آن، n تعداد DNNها در VEE را نشان می‌دهد. با در نظر گرفتن سرعت آموزش، محدودیت حافظه GPU و دقت پیش‌بینی VEE، ما از شش شبکه عصبی یکسان برای ساخت VEE استفاده می‌کنیم و میانگین احتمالات تولیدشده توسط این شش DNN را به‌ عنوان پیش‌بینی مدل در نظر می‌گیریم.

با گرفتن میانگین وزنی تمام DNNها، می‌توانیم نقص شناختی (Cognitive Defects) یک DNN منفرد ناشی از تصادفی بودن نمونه‌گیری در نواحی خاص را کاهش دهیم.

4.2.3 تعیین انتقال مسیر از توزیع پیش‌بینی‌ شده (Determine the Path Transition from the Predicted Distribution)

با داشتن ورودی (pt, at)، DNNها انتقال‌های مسیر بالقوه و پاداش‌های متناظر را به صورت (pt+1, rt) و با توزیع احتمال گاوسی خروجی می‌دهند.

با این حال، در DGF، جهش یک بذر تنها موجب یک انتقال مسیر مشخص می‌شود. بنابراین، ما از روش نمونه‌گیری تصادفی (Random Sampling) برای تعیین مسیر بعدی pt+1 استفاده می‌کنیم، که بر اساس احتمال‌های پیش‌بینی‌شده انتقال‌های مسیر مختلف انجام می‌شود.

4.3 مدل یادگیری تقویتی برای فازینگ (Reinforcement Learning for Fuzzing – RLF)

برای هدایت مؤثرتر فازر به سمت نقطه هدف، یعنی از طریق توالی‌های انتقال مسیر با پاداش بالا (High-Reward Path Transition Sequences)، لازم است یک سیاست (Policy) بیاموزیم که اقدامات را برای بیشینه کردن پاداش توالی (Sequence Rewards) انتخاب کند.

با توجه به تعداد بسیار زیاد مسیرها، اقدامات و انتقال‌های مسیر در مدل انتقال مسیر، استفاده از روش‌های ریاضی سنتی مانند برنامه‌ریزی پویا (Dynamic Programming – DP) [6] برای یادگیری سیاست و محاسبه پاداش‌های توالی مورد انتظار دشوار است.

بنابراین، ما مدل Reinforcement Learning for Fuzzing (RLF) را توسعه دادیم که مبتنی بر الگوریتم یادگیری تقویتی Soft Actor-Critic (SAC) [28] است.

4.3.1 طراحی مدل RLF

همان‌طور که در شکل ۲ نشان داده شده است، بر اساس ساختار SAC، مدل RLF شامل سه شبکه اصلی است:

شبکه Actor
شبکه Q-Critic
شبکه V-Critic

در طول فرایند آموزش:

شبکه Q-Critic برای ارزیابی پاداش توالی مورد انتظار (Expected Sequence Reward) آموزش داده می‌شود.
شبکه V-Critic برای ارزیابی مقدار انتقال (Transition Value) هر مسیر آموزش داده می‌شود.

با استفاده از پاداش‌های توالی مورد انتظار و مقادیر انتقال، شبکه Actor آموزش می‌بیند تا سیاست (Policy) را بهینه کند و احتمال انتخاب اقداماتی با پاداش توالی مورد انتظار بالا را افزایش دهد.

4.3.2 پردازش و جمع‌آوری داده‌های آموزشی

ما مدل انتقال مسیر را به‌عنوان محیط در یادگیری تقویتی در نظر می‌گیریم و فازر، مسیر، عمل، انتقال مسیر و پاداش در مدل انتقال مسیر را به ترتیب به عامل، حالت، عمل، انتقال حالت و پاداش در یادگیری تقویتی نگاشت می‌کنیم. علاوه بر این، RLF روش رمزگذاری مسیر، عمل و پاداش را از VEE مجدداً استفاده می‌کند. از آنجا که ما انتقال‌های مسیر تاریخی و انتقال‌های مسیر پیش‌بینی‌شده را برای آموزش RLF ترکیب می‌کنیم تا مدل RLF بتواند آینده‌نگری (foresight) داشته باشد، بنابراین انتقال‌های مسیر تاریخی و پیش‌بینی‌شده را به روش‌های متفاوت جمع‌آوری می‌کنیم.

جمع‌آوری انتقال‌های مسیر تاریخی (Collecting historical path transitions). از آنجا که محیط DGF با محیط فرایند یادگیری تقویتی سنتی که در آن انتقال‌های حالت به‌صورت سریالی تولید و به شکل (s0, a0, s1, a1, …, an−1, sn)، نمایش داده می‌شوند متفاوت است، پردازش داده‌های آموزشی RLF با یادگیری تقویتی سنتی (مثلاً SAC) متفاوت است. در DGF، فازر ممکن است یک بذر را چندین بار جهش دهد که منجر به انتقال‌های مسیر متفاوت از همان مسیر می‌شود. این به آن معناست که فازر می‌تواند روی یک مسیر مشخص باقی بماند و اقدامات مختلفی انجام دهد تا انتقال‌های مسیر متفاوتی ایجاد کند. بنابراین، برای مدل RLF، دستیابی به یک توالی کامل از انتقال‌های مسیر و ارزیابی کارایی سیاست جاری با محاسبه پاداش توالی در یک بازه کوتاه (مثلاً چند ثانیه) عملی نیست.

بر اساس این ملاحظات، در هر چرخه فازینگ (Fuzzing Cycle)، فازر اقدامات را مطابق با سیاست انتخاب می‌کند تا انتقال‌های مسیر ایجاد شود. انتقال‌های مسیر تاریخی در بافر بازپخش تاریخی (Historical Replay Buffer) ذخیره می‌شوند و توسط مدل RLF در پایان چرخه فازینگ بارگذاری می‌شوند تا RLF در چرخه فازینگ بعدی آموزش داده شود.

جمع‌آوری انتقال‌های مسیر پیش‌بینی‌ شده (Collecting predicted path transitions): ما از VEE برای شبیه‌سازی مدل انتقال مسیر استفاده می‌کنیم و از استراتژی k-step branch rollout برای به‌دست آوردن انتقال‌های مسیر پیش‌بینی‌شده که هنوز در مدل انتقال مسیر رخ نداده‌اند بهره می‌بریم. در استراتژی k-step branch rollout، مدل RLF به‌عنوان عامل در نظر گرفته می‌شود و در هر مسیر، مطابق با سیاست اولیه، یک توالی از اقدامات را انتخاب می‌کند تا k انتقال مسیر ایجاد شود و یک توالی انتقال مسیر جدید با طول k تولید گردد.

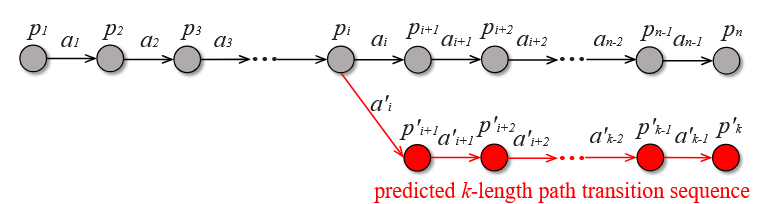
ما از شکل 3 برای نشان دادن فرآیند استراتژی گسترش شاخه k مرحله‌ای استفاده میکنیم. فرض کنید (p0,a0,p1,a1…pi,ai,…an−1,pn) یک دنباله انتقال مسیر تاریخی در مدل انتقال مسیر باشد. ما انتقالها را در نظر میگیریم و یک دنباله انتقال مسیرk مرحله‌ای جدید ایجاد میکنیم که به صورت (pi, a′ i, ri, p′ i+1), (p′ i+1, a′ i+1, r′ i+1, p′ i+2), … , (p′ i+k−1, a′ i+k−1, r′ i+k−1, p′ i+k) نمایش داده میشود. در اینجا، k یک ابرپارامتر (Hyperparameter) است که دقت پیش‌بینی‌های VEE و آینده‌نگری (Foresight) سیاست طراحی‌شده توسط مدل RLF را تحت تأثیر قرار می‌دهد.

پیش بینی‌ها ممکن است نیاز داشته باشند که چندین مورد آزمایشی (Testcase) را در طول فرآیند راه اندازی شاخه k مرحله‌ای پوشش دهند. در بین تست‌کیس‌های مختلف، همان اقدامات تعریف‌شده توسط مکان بایت‌ها ممکن است ناهم‌تراز (Misaligned) باشند، به این معنا که مکان بایت جهش داده‌شده در یک مورد آزمایشی ممکن است با بایت جهش داده‌ شده در مورد آزمایشی دیگر به دلیل طول متفاوت موارد آزمایشی متفاوت باشد. برای مدیریت این ناهم‌ترازی، از عبارت زیر استفاده می‌کنیم تا تست‌ کیس‌های میانی مختلف تولیدشده در طول فرآیند را از هم متمایز کنیم: ID ∧ (path ID >> 2).

به عنوان مثال، برای موارد آزمایشی 1 و 2 که مسیر یکسانی را پوشش می‌دهند، ما به آن‌ها شناسه‌های متفاوت اختصاص می‌دهیم تا بتوانیم جهش‌ها روی موارد آزمایشی میانی مختلف را تفکیک کنیم. به این ترتیب، حتی اگر همان بایت در موارد آزمایشی 1 و 2 جهش داده شود، ما احتمال‌ها و پاداش‌های مرتبط با انتقال مسیر ناشی از این دو جهش را یکسان در نظر نمی‌گیریم.

4.3.3 آموزش مدل RLF

مدلRLF انتقال‌های مسیر تاریخی و انتقال‌های مسیر پیش‌بینی‌شده را ترکیب می‌کند تا شبکه Actor، شبکه Q-Critic و شبکه V-Critic آموزش داده شوند. در DGF، هدف ما این است که فازر اقداماتی را با پاداش توالی مورد انتظار بالا انتخاب کند و در عین حال اقدامات مختلفی را برای ایجاد انتقال‌های مسیر جدید کاوش کند. بنابراین، در RLF، از آنتروپی (Entropy) برای سنجش تصادفی بودن انتخاب اقدامات استفاده می‌کنیم.

فرض کنید اقدامات در حالت st بر اساس سیاست π انتخاب می‌شوند و احتمال‌های انتخاب اقدامات از یک توزیع پیروی می‌کنند که با π(·|st) نمایش داده می‌شود، آنگاه آنتروپی اقدام به صورت زیر محاسبه می‌شود:

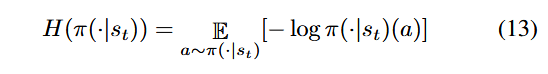
در مدل RLF، هدف شبکه Actor این است که یک سیاست ∗π بیاموزد که هم پاداش (Reward) و هم آنتروپی (Entropy) را بیشینه (maximize) کند.

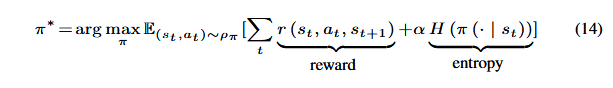
که در آن، α ضریبی است که کاوش (Exploration) و بهره‌برداری (Exploitation) را متعادل می‌کند، همان‌طور که در SAC پیشنهاد شده است. سپس، ما تابع هدف (Objective Function) برای شبکه Q-Critic و تابع هدف برای شبکه V-Critic را تعریف می‌کنیم تا پارامترهای ω شبکه Q-Critic و پارامترهای ϕ شبکه V-Critic آموزش داده شوند.

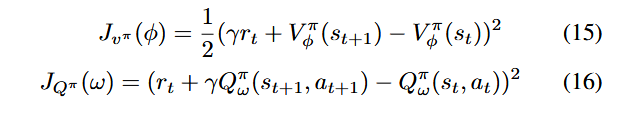
برای شبکه Actor، ما پارامترهای σ شبکه Actor را آموزش می‌دهیم تا پاداش توالی مورد انتظار اقدامات را بیشینه کنند، به طوری که پاداش توالی کل (Sequence Rewards) نیز بیشینه شود.

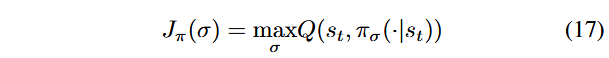
با کمینه کردن این سه تابع هدف، ما پارامترهای سه شبکه را آموزش می‌دهیم تا بتوانند پاداش‌های توالی مورد انتظار (Expected Sequence Rewards) و مقادیر انتقال (Transition Values) را محاسبه کنند و سیاستی برای انتخاب اقدامات طراحی کنند که بتواند پاداش‌های توالی را بیشینه کند.

مدل RLF آموزش‌دیده، دو نوع اطلاعات بهینه‌سازی را به مولفه FO ارائه می‌دهد:

پاداش‌های توالی مورد انتظار و مقادیر انتقال تخمینی
سیاست انتخاب اقدامات در هر مسیر

4.4 بهینه‌سازی استراتژی‌های فازینگ بر اساس گروه اقدام (Optimize Fuzzing Strategies Based on Action Group)

برای هدایت فازر به منظور اجرای توالی‌های انتقال مسیر بهینه با بیشترین پاداش توالی، لازم است استراتژی‌های فازینگ را بر اساس اطلاعات بازخورد از مدل RLF بهینه کنیم. در سال‌های اخیر، تکنیک‌های پیشرفته‌ای برای بهینه‌سازی یک استراتژی فازینگ منفرد پیشنهاد شده‌اند، مانند انتخاب بذر (Seed Selection) [12]، برنامه زمان‌بندی جهش‌گرها (Mutator Schedule) [48] و انتخاب مکان جهش (Mutation Location Selection) [69].

با این حال، بهینه‌سازی یک استراتژی منفرد فازینگ ممکن است به طور قابل توجهی فازر را به سمت توالی‌های انتقال مسیر بهینه هدایت نکند. بنابراین، ما مفهوم گروه اقدام (Action Group) را معرفی می‌کنیم که از پنج عنصر تشکیل شده و تلاش می‌کنیم چندین استراتژی فازینگ را به صورت جامع بهینه کنیم. علاوه بر این، ما الگوریتم بهینه‌سازی دسته‌ای ذرات چندعنصری (Multi-elements Particle Swarm Optimization – MPSO) را پیشنهاد می‌کنیم تا عناصر گروه اقدام را به‌طور همزمان بهینه‌سازی کند.

4.4.1 مفهوم گروه اقدام (The Concept of Action Group)

ما گروه اقدام را به‌صورت یک تاپل متشکل از پنج عنصر تعریف می‌کنیم:

انتخاب بذر (Seed-Selection – SS): نمایانگر احتمال انتخاب یک بذر توسط فازر برای فازینگ است.
انرژی بذر (Seed-Energy – SE): نمایانگر انرژی اختصاص داده‌شده به بذر است که تعیین می‌کند چه تعداد جهش می‌توان روی بذر در مرحله havoc اعمال کرد.
تعداد دورهای havoc (Havoc-Round – HR): نمایانگر تعداد دورهای حلقه‌ای است که برای انتخاب جهش‌گرها و بایت‌های مختلف در مرحله havoc استفاده می‌شود. همه جهش‌گرها و بایت‌های انتخاب‌شده در یک اقدام واحد havoc ادغام می‌شوند. مقدار Havoc-Round می‌تواند یکی از اعداد ۲، ۴، ۸، ۱۶، ۳۲، ۶۴ یا ۱۲۸ باشد.
جهش‌گر (Mutator – MT): نمایانگر جهش‌گری است که برای جهش بذر انتخاب می‌شود. مشابه AFL [39]، DeepGo از ۱۶ نوع جهش‌گر مختلف پشتیبانی می‌کند.
مکان جهش (Location – LC): نمایانگر مکان بایت بذر است که برای جهش انتخاب می‌شود.

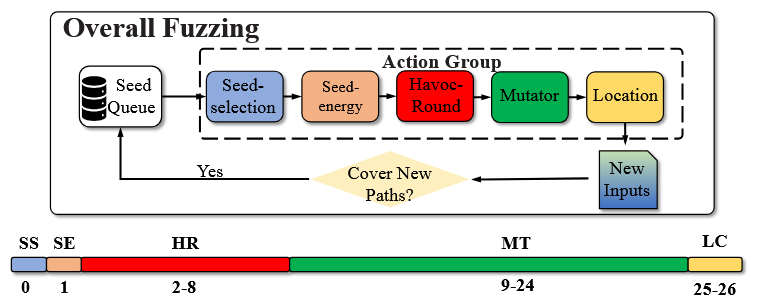
هر گروه اقدام به‌صورت یک بردار ۲۷ بعدی نمایش داده می‌شود که از ۵ عنصر تشکیل شده است. همان‌طور که در شکل ۴ نشان داده شده، SS و SE هر دو بردار ۱ بعدی هستند. مقدار SS نشان‌دهنده احتمال انتخاب بذر برای فازینگ در بازه [0,1][0, 1][0,1] است و فازر بر اساس آن بذرها را برای فازینگ انتخاب می‌کند. مقدار SE نشان‌دهنده انرژی اختصاص داده‌شده به بذر است و فازر بر اساس آن تعداد دفعات جهش بذرها را محاسبه می‌کند.

HR یک بردار ۷ بعدی است که هر بعد آن احتمال انتخاب یکی از هفت مقدار مختلف havoc-round (۲، ۴، ۸، ۱۶، ۳۲، ۶۴ و ۱۲۸) را نمایش می‌دهد. فازر تعداد دورهای حلقه‌ای مورد استفاده برای انتخاب جهش‌گرها و مکان‌های جهش را در مرحله havoc بر اساس HR نمونه‌گیری می‌کند.

MT یک بردار ۱۶ بعدی است که هر بعد آن احتمال انتخاب یکی از ۱۶ نوع جهش‌گر مختلف را نشان می‌دهد.

LC یک بردار ۲ بعدی است که بعد اول آن احتمال انتخاب مکان‌های بهینه (Optimal Locations) و بعد دوم آن احتمال انتخاب مکان‌های معمولی (Common Locations) را نشان می‌دهد. ما مکان‌های جهش بذرها را به دو دسته تقسیم می‌کنیم: مکان‌های بهینه و مکان‌های معمولی. مکان‌های بهینه شامل مکان‌های جهشی است که توسط سیاست مدل RLF با احتمال بیش از ۸۰٪ انتخاب شده‌اند، در حالی که مکان‌های معمولی شامل تمام مکان‌های جهش دیگر است.

بر اساس MT و LC، فازر جهش‌گرها و نوع مکان جهش را نمونه‌گیری می‌کند. فازر به‌طور مداوم بذرها را جهش می‌دهد تا ورودی‌های جدید تولید کند بر اساس ۵ عنصر موجود در گروه اقدام. همان‌طور که در شکل ۴ نشان داده شده، ما هر عنصر را به‌صورت یک بردار نمایش می‌دهیم و سپس پنج بردار را به هم الحاق می‌کنیم تا یک بردار واحد برای نمایش گروه اقدام یک بذر ایجاد شود.

4.4.2 الگوریتم بهینه‌سازی دسته‌ای ذرات چند عنصری (Multi-elements Particle Swarm Optimization – MPSO):

برای بهینه‌سازی همزمان پنج عنصر موجود در گروه اقدام، ما هر گروه اقدام (action group) را به‌ عنوان یک ذره نمایش می‌دهیم که با یک بردار ۲۷ بعدی مشخص می‌شود و بهینه‌سازی گروه اقدام را به‌صورت یک مسأله بهینه‌سازی چند عنصری (Multi-element Optimization Problem) در نظر می‌گیریم.

ما الگوریتم بهینه‌سازی دسته‌ای ذرات چندعنصری (MPSO) را برای تحقق این بهینه‌سازی پیشنهاد می‌کنیم. بهینه‌سازی گروه اقدام می‌تواند فازر را به سمت توالی‌های انتقال مسیر مطلوب با پاداش توالی بالا هدایت کند.

همان‌طور که در فصل دوم معرفی شد، الگوریتم PSO از ذرات بدون جرم (Massless Particles) برای شبیه‌سازی پرندگان در یک دسته استفاده می‌کند. هر ذره به‌صورت مستقل به دنبال یافتن راه‌حل بهینه می‌گردد و آن را به‌ عنوان مقدار بهترین محلی (Local Best Value) ثبت می‌کند. سپس مقادیر بهترین محلی میان تمام ذرات در کل دسته (Swarm) به اشتراک گذاشته می‌شود تا بهترین مقدار جهانی (Global Best Value) به‌ عنوان راه‌حل بهینه پیدا شود.

هر ذره دو ویژگی اصلی دارد: سرعت (Velocity) و موقعیت (Position). سرعت نشان‌ دهنده سرعت حرکت و موقعیت نشان‌دهنده جهت حرکت است. تمام ذرات در دسته به‌طور مداوم سرعت و موقعیت خود را بر اساس بهترین مقدار محلی و بهترین مقدار جهانی که در کل دسته به اشتراک گذاشته شده است، تنظیم می‌کنند:

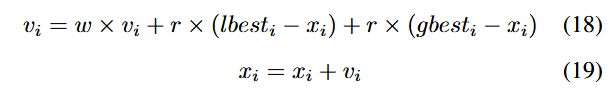
که در آن، vi نشان‌دهنده سرعت ذره iام و xi نشان‌دهنده موقعیت ذره iام است، r وزن جابجایی تصادفی در بازه [0,1][0,1][0,1] را نشان می‌دهد، lbestilbest_ilbesti بهترین موقعیت محلی (local best position) یافت‌شده توسط ذره iام است و gbestigbest_igbesti بهترین موقعیت جهانی (global best position) یافت‌شده توسط تمام ذرات را نمایش می‌دهد.

ضریب اینرسی ω مقداری غیرمنفی است که مقدار بالاتر آن باعث قوی‌تر شدن بهینه‌سازی جهانی و ضعیف‌تر شدن توانایی بهینه‌سازی محلی (لوکال) در الگوریتم PSO می‌شود. در این مقاله، ما از روش وزن اینرسی کاهش‌یابنده خطی (Linearly Decreasing Inertia Weight – LDIW) [70] برای تعیین مقدار ω استفاده می‌کنیم:

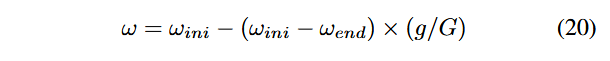
که در آن، ωini و ωend به‌ ترتیب نشان‌دهنده مقدار اینرسی اولیه و مقدار اینرسی نهایی هستند. بر اساس روش LDIW، معمولاً ωini و ωend به ترتیب برابر ۰.۴ و ۰.۹ تنظیم می‌شوند. g نشان‌دهنده تعداد تکرارهای انجام‌شده توسط ذره جاری است که برابر با تعداد جهش‌هایی است که فازر روی بذر (seed) متناظر انجام داده است. G نشان‌دهنده حداکثر تعداد تکرارها است که برابر با کل دفعات جهش محاسبه‌شده بر اساس انرژی بذر (seed) می‌باشد. در DeepGo، تعداد دفعات جهش بذرها توسط انرژی اختصاص داده‌شده به بذرها تعیین می‌شود.

بهترین موقعیت محلی و کارایی محلی (Local Best Position and Local Efficiency): در الگوریتم MPSO، هر ذره دارای بهترین موقعیت محلی lbest و کارایی محلی ef flocal خود است. برای یک ذره مشخص، موقعیت x1 تنها زمانی برتر از موقعیت x2 محسوب می‌شود که کارایی محلی به‌دست‌آمده توسط ذره در x1 از کارایی محلی در x2 بیشتر باشد.

ما از کارایی محلی برای کمی‌سازی کارایی جهش‌های استراتژی‌های فازینگ که از پنج عنصر تشکیل شده‌اند، برای یک ذره مشخص استفاده می‌کنیم. کارایی محلی بر اساس میانگین پاداش‌های توالی مورد انتظار (Expected Sequence Rewards) تمام جهش‌هایی که فازر در مسیر متناظر با ذره انجام داده است، محاسبه می‌شود.

در DGF، هر جهش روی بذر منجر به یک انتقال مسیر از p به ′p می‌شود. مطابق معادله ۸، در هر انتقال مسیر، از عبارت r + γV t π (p′) برای ارزیابی پاداش‌های توالی مورد انتظار استفاده می‌کنیم. بر اساس این مقدار، کارایی محلی محاسبه می‌شود.

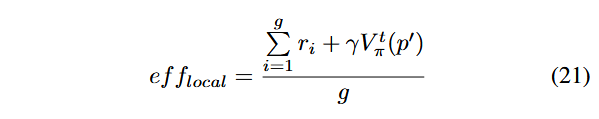
که در آن، V t π (p′) نشان‌دهنده مقدار انتقال (Transition Value) مسیر p′ است که توسط جهش iام پوشش داده شده است.

موقعیت بهترین جهانی و کارایی جهانی (Global Best Position and Global Efficiency): ما از کارایی جهانی (Global Efficiency) برای کمی‌سازی کارایی فازینگ فازر استفاده می‌کنیم. از آنجا که کارایی جهانی فازر به کارایی محلی ذرات مختلف و روابط بین ذرات بستگی دارد، موقعیت جهانی همه ذرات را بر اساس کارایی فازینگ در یک چرخه فازینگ تعیین می‌کنیم.

یک ذره (particle) تنها زمانی در موقعیت بهترین جهانی (gbest) قرار دارد که کارایی فازینگ فازر در آن موقعیت از کارایی هر موقعیت دیگر بیشتر باشد. ما از میانگین پاداش‌های توالی در طول چرخه فازینگ برای ارزیابی کارایی جهانی استفاده می‌کنیم:

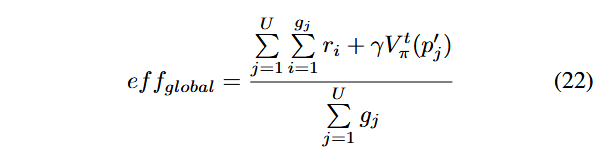
که در آن، fglobal نشان‌دهنده کارایی جهانی است، pj نشان‌دهنده بذر jام، gj نشان‌دهنده کل تعداد جهش‌ها برای pj و U نشان‌دهنده تعداد بذرهایی است که در چرخه فازینگ جاری مورد فازینگ قرار گرفته‌اند.

الگوریتم MPSO:

				
					Input: Ω(s,p)
Output: Us, Ω(s,p′)
	Initial(Ω(s,p))
	while f uzzing do
		for (si, pi) in Ω(s,p) do
			if P rob Sels(pi(SS)) == True then
				mni ←Cal_MN(pi(SE))
				for j in mni do
					hrj ← $P rob Selh(pi(HR), hmj ←<>
					for k in hrj do
						lck ← P rob Sell(pi(LC)),
						mtk ← P rob Selm(pi(MT)),
						hmj ← hmj ∪ (lck , mtk )
					end for
					new input = Mutate(hmj , si)
					ef flocal, ef fglobal = Cal_eff(si, new input)
					Update(lbest, gbest, pi)
				end for
			end if
		end for
	end while

در طول فرآیند فازینگ، ما کارایی محلی و کارایی جهانی ذرات را مطابق با معادلات (۲۱) و (۲۲) محاسبه کرده و lbest و gbest را ثبت می‌کنیم. سپس موقعیت‌های فضایی ذرات را بر اساس معادلات (۱۸)، (۱۹) و (۲۰) به‌روزرسانی می‌کنیم و تمام ذرات را به سمت جهت‌های lbest و gbest حرکت می‌دهیم.

با این رویکرد، ما گروه‌های اقدام تمام بذرها را بهینه‌سازی می‌کنیم تا فازر را از طریق توالی‌های انتقال مسیر بهینه به هدف هدایت کنیم.

فرآیند MPSO در الگوریتم ۱ نشان داده شده است، که در آن، s نشان‌دهنده بذر، p نشان‌ دهنده ذره و Ω(s,p) مجموعه‌ای است که تمام بذرها و ذرات متناظر آن‌ها را شامل می‌شود. تابع Prob_Sels مشخص می‌کند که آیا بر اساس مقدار SS، بذر باید فاز شود یا خیر.mni نشان‌دهنده تعداد دفعات جهش بذر است و تابع Cal_MN تعداد دفعات جهش بذر را بر اساس SE محاسبه می‌کند.

توابع ProbSelh ،ProbSell و ProbSelm به ترتیب به‌صورت احتمالی مقادیر مربوط به hr برای HR، lc برای مکان جهش بر اساس LC و mt برای جهش‌گر بر اساس MT را انتخاب می‌کنند.

در ابتدا، پنج عنصر در تمام ذرات مقداردهی اولیه می‌شوند (خط ۱). برای SS و SE بر اساس ویژگی‌های بذرها (مانند اندازه bitmap و سرعت اجرا)، AFL [39] احتمال انتخاب بذرها برای فازینگ و انرژی اختصاص داده‌ شده به بذرها را محاسبه می‌کند. ما از احتمال‌ها و انرژی بذر به‌دست‌آمده از روش AFL به‌عنوان مقدار اولیه SS و SE استفاده می‌کنیم.

برای HR ،LC و MT از میانگین احتمال به‌عنوان مقدار اولیه موقعیت فضایی آن‌ها استفاده می‌کنیم (مثلاً 1/16 برای هر جهش‌گر). در طول فرآیند فازینگ، فازر به ترتیب:

بذرها را بر اساس SS برای فازینگ انتخاب می‌کند (خط ۴).
تعداد دفعات جهش را بر اساس SE محاسبه می‌کند (خط ۵).
مقادیر HR (یعنی hrjhr_jhrj) را انتخاب می‌کند (خط ۷).
بایت‌های بذر برای جهش (یعنی lcklc_klck) را بر اساس LC انتخاب می‌کند (خط ۹).
جهش‌گرها (یعنی mtkmt_kmtk) را بر اساس MT انتخاب می‌کند (خط ۱۰).

در هر چرخه hrj ،mtk و lck با هم ترکیب می‌شوند تا جهش havoc (یعنی hmj) ایجاد شود (خط ۱۱) و فازر از hmj برای جهش بذر si و تولید ورودی جدید استفاده می‌کند (خط ۱۳). سپس، MPSO کارایی محلی و کارایی جهانی را محاسبه می‌کند (خط ۱۴) و lbest، gbest و موقعیت ذره pi را به‌روزرسانی می‌کند (خط ۱۵).

قابل توجه است که مقدار تمام ابعاد ذره به طور مداوم بر اساس معادلات (۱۸)، (۱۹) و (۲۰) تغییر می‌کند تا موقعیت فضایی ذره به‌روز شود و ذره به سمت lbest و gbest حرکت کند.

برای مثال، اگر یک ذره کارایی محلی پایینی داشته باشد که منجر به کاهش کارایی جهانی فازر شود، بر اساس معادلات (۱۸)، (۱۹) و (۲۰)، مقادیر SS و SE به‌تدریج در طول فرآیند MPSO کاهش می‌یابند.

به محض اینکه کامپوننت FO اولین بار اطلاعات بازخورد را از مدل RLF دریافت کند، الگوریتم MPSO اجرا خواهد شد و تا پایان فرآیند فازینگ ادامه خواهد یافت.

5. پیاده‌سازی

پیاده‌سازی DeepGo عمدتاً از سه کامپوننت تشکیل شده است: فازر، VEE، و مدل RLF. برای آنالیزور استاتیک در فازر، از LLVM نسخه ۱۱.۰ استفاده می‌کنیم. ما از LLVM IR برای ابزارگذاری برنامه و دریافت اطلاعاتی مانند فاصله در سطح بلاک‌های پایه و شاخه‌های هم‌خانواده بهره می‌بریم.

فازر بر پایه AFLGo ساخته شده و شامل ۲۱۰۰ خط کد C است، و VEE و مدل RLF با حدود ۱۳۰۰ خط کد Python پیاده‌سازی شده‌اند.

به‌طور جزئی، شبکه‌های عصبی VEE در PyTorch 1.13.0 با پنج لایه کاملاً متصل (fully connected) پیاده‌سازی شده‌اند. لایه‌های مخفی از تابع فعال‌سازی Swish استفاده می‌کنند. شبکه‌ها برای ۵۰۰ دوره آموزش داده می‌شوند و از ابزار tensorboard برای نظارت خودکار بر مقادیر زیان (Loss) بهره می‌بریم تا مشخص شود آیا به مقدار کوچکی همگرا می‌شوند یا خیر. در صورتی که مقادیر Loss در VEE و RLF همگرا شوند، شبکه‌ها به‌ طور خودکار آموزش را متوقف می‌کنند.

شبکه‌های مدل RLF شامل سه لایه کاملاً متصل هستند. برای ابرپارامترهای مدل RLF، با مراجعه به تنظیمات نرخ یادگیری برای Q-Critic، V-Critic و Actor در SAC، مقدار ۰.۰۰۵ تنظیم شده است تا کارایی یادگیری و همگرایی مدل RLF تضمین شود (در فرآیند آزمایش، هر سه شبکه به سرعت همگرا می‌شوند).

نکتهٔ قابل توجه این است که هنگام استفاده از DeepGo برای تست برنامه‌ها، فرآیند فازینگ، آموزش مدل‌ها و پیش‌بینی انتقال مسیرها به‌صورت هم‌زمان انجام می‌شوند. ما از یک GPU اضافی برای آموزش مدل‌های VEE و RLF بر اساس اطلاعاتی که در طول فرآیند فازینگ جمع‌آوری می‌شود استفاده می‌کنیم. تمام زمانی که صرف آموزش و پیش‌بینی توسط مدل‌های VEE و RLF می‌شود، به‌عنوان بخشی از بودجهٔ زمانی فرآیند فازینگ محاسبه می‌شود (که به‌صورت wall clock time در نظر گرفته شده است).

6. ارزیابی

به‌منظور ارزیابی اثربخشی DeepGo، آزمایش‌هایی انجام دادیم که هدف آن‌ها پاسخ به پنج سؤال پژوهشی زیر است:

RQ1: عملکرد DeepGo از نظر رسیدن به مکان‌های کد هدف چگونه است؟
RQ2: عملکرد DeepGo از نظر آشکارسازی آسیب‌پذیری‌های شناخته‌شده چگونه است؟
RQ3: عملکرد VEE در پیش‌بینی احتمال‌ها و پاداش‌های انتقال مسیرها چگونه است؟
RQ4: آیا مدل RLF و مؤلفه FO می‌توانند فازر را به سمت توالی‌های انتقال مسیر با پاداش تجمعی بالا هدایت کنند؟
RQ5: مؤلفه‌های VEE، RLF و FO چه سهمی در عملکرد کلی DeepGo دارند؟

6.1 تنظیمات ارزیابی

معیارهای ارزیابی. برای ارزیابی عملکرد تکنیک‌های مختلف فازینگ، از دو نوع معیار استفاده می‌کنیم:

Time-to-Reach (TTR) برای ارزیابی زمانی به‌کار می‌رود که صرف تولید اولین ورودی‌ای می‌شود که بتواند به مکان کد هدف برسد.
Time-to-Expose (TTE) برای ارزیابی زمانی استفاده می‌شود که صرف آشکارسازی آسیب‌پذیری‌ها (شناخته‌شده یا افشانشده) در مکان‌های کد هدف می‌گردد. وقوع یک کرش مشاهده‌شده نشان می‌دهد که فازر با موفقیت آسیب‌پذیری را آشکار کرده است.

بنچمارک‌های ارزیابی. ما دو مجموعه‌داده را انتخاب کردیم که به‌طور گسترده توسط تکنیک‌های پیشرفته فازینگ خاکستری جهت‌دار (DGF) مورد استفاده قرار گرفته‌اند (برای مثال، WindRanger [22] و BEACON [31]).

UniBench‏[43] برنامه‌های دنیای واقعی از انواع مختلف به‌همراه مجموعه بذر متناظر را فراهم می‌کند. تکنیک‌های پیشرفته فازینگ، مانند WindRanger، از UniBench به‌عنوان بنچمارک ارزیابی استفاده کرده‌اند. برای پاسخ به RQ1، RQ3، RQ4 و RQ5، ما ۲۰ برنامه از UniBench را مورد آزمایش قرار دادیم و با انجام آزمایش‌های مقدماتی، از ++AFL ‏[23] برای انتخاب مکان‌های کد هدف در هر برنامه استفاده کردیم. بدین‌صورت که ابتدا ++AFL را به‌مدت ۴۸ ساعت اجرا کرده و تمامی بذرهای تولیدشده توسط ++AFL را جمع‌آوری کردیم. سپس با استفاده از afl-cov این بذرها را مجدداً اجرا کردیم تا بتوانیم مکان‌های کدی که پوشش داده شده‌اند و زمان پوشش آن‌ها را به‌دست آوریم؛ این اطلاعات به‌شکل زوج‌هایی مانند (line, time) نمایش داده می‌شوند. در نهایت، از میان مکان‌هایی که زمان رسیدن به آن‌ها بین ۱ ساعت تا ۴۸ ساعت بوده است (یعنی بیش از ۱ ساعت)، به‌صورت تصادفی ۴ مکان کد را به‌عنوان اهداف انتخاب کردیم.
AFLGo testsuite‏[12] در مقاله و وب‌سایت AFLGo برای ارزیابی «جهت‌مندی» فازینگ خاکستری هدایت‌ شده (DGF) معرفی شده است. این مجموعه آزمون توسط تکنیک‌های پیشرفته DGF به‌ عنوان بنچمارک مورد استفاده قرار گرفته تا قابلیت بازتولید باگ‌ها را بررسی کنند. برای پاسخ به RQ2، ما AFLGo testsuite را به‌عنوان بنچمارک انتخاب کردیم تا توانایی DeepGo در آشکارسازی آسیب‌پذیری‌های شناخته‌شده را ارزیابی کنیم.

خطوط پایه (Baselines). ما در ارزیابی خود، DeepGo را با فازرهای خاکستری هدایت‌شدهٔ پیشرفته‌ای که در زمان نگارش این مقاله به‌صورت عمومی در دسترس بودند مقایسه کردیم؛ از جمله WindRanger، BEACON، ParmeSan و AFLGo.

تنظیمات آزمایش. ما آزمایش‌ها را روی سیستمی مجهز به پردازنده Intel(R) Xeon(R) Gold 6133 CPU @ 2.50GHz با ۸۰ هسته و سیستم‌عامل Ubuntu 20.04 LTS انجام دادیم. تمامی آزمایش‌ها ۵ بار تکرار شدند و برای هر بار، بودجه زمانی ۲۴ ساعت در نظر گرفته شد. هنگام آزمون برنامه‌های موجود در UniBench و مجموعه‌آزمون AFLGo، از بذرهای (seed) موجود در seed corpus پیشنهادی بنچمارک به‌عنوان بذر اولیه استفاده کردیم. برای تحلیل نتایج آزمایش‌ها، از آزمون Mann–Whitney U (مقدار p) برای سنجش معناداری آماری استفاده کردیم. علاوه بر این، از آماره Vargha–Delaney ‏(Â12)‏ [4] برای اندازه‌گیری احتمال عملکرد بهتر یک تکنیک نسبت به تکنیک دیگر بهره گرفتیم.

6.2 رسیدن به نقاط هدف

برای پاسخ به RQ1، ما ۲۰ برنامه از UniBench را با مجموع ۸۰ نقطهٔ هدف مورد آزمایش قرار دادیم و مقدار TTR فازرهای مختلف را ارزیابی کردیم. آستانهٔ زمان پایان (timeout) برابر با ۲۴ ساعت تنظیم شد. نتایج تفصیلی TTR در جدول III در پیوست ارائه شده‌اند. در جدول 3، ورودی «N/A» نشان‌ دهندهٔ آن است که فازر به دلیل مشکلات کد موفق به کامپایل برنامه نشده است، در حالی که «T.O.» بیانگر آن است که فازر نتوانسته است در بازهٔ زمانی اختصاص‌یافتهٔ ۲۴ ساعته به نقطهٔ هدف برسد. در مورد WindRanger، برخی ورودی‌ها به دلیل بروز خطاهای segmentation fault یا ناتوانی در به‌دست‌آوردن اطلاعات فاصله در حین آزمون برنامه با «N/A» مشخص شده‌اند. در خصوص BEACON و ParmeSan، بخش عمده‌ای از ورودی‌های «N/A» احتمالاً به این دلیل است که این ابزارها با UniBench سازگار نیستند. برای ورودی‌های «N/A»، از آن‌ها در محاسبهٔ ضریب تسریع (speedup) و مقادیر p استفاده نکردیم. در مورد ورودی‌های «T.O.»، بر این باوریم که این فازرها ممکن است در فرآیندهای فازینگ بعدی به اهداف برسند؛ بنابراین، برای محاسبهٔ speedup و مقادیر p، مقدار اندکی بزرگ‌تر برابر با ۱۵۰۰ دقیقه را در نظر گرفتیم.

بر اساس نتایج TTR، DeepGo در مقایسه با AFLGo ‏(22/80)، BEACON ‏(11/80)، WindRanger ‏(19/80) و ParmeSan ‏(9/80)، می‌تواند بیشترین تعداد از نقاط هدف یعنی 73 مورد از 80 را در محدودهٔ زمانی تعیین‌شده پوشش دهد. علاوه بر این، در اغلب نقاط هدف (67 مورد از 80)، DeepGo عملکردی بهتر از سایر فازرها دارد و کوتاه‌ترین زمان رسیدن به هدف را به دست می‌آورد.

از نظر میانگین TTR برای رسیدن به نقاط هدف، DeepGo به‌ ترتیب نسبت به AFLGo، BEACON، WindRanger و ParmeSan بهبود سرعتی برابر با ×3.23, ×1.72, ×1.81 و ×4.83 نشان می‌دهد. ما هر دو آزمون آماری Mann-Whitney U (بر اساس مقدار p-value) و Vargha-Delaney ‏( ˆA12 ) را اجرا کردیم که در آن‌ها تمام مقادیر p-value کمتر از 0.05 بوده و مقادیر میانگین ˆA12 در مقایسه با AFLGo، BEACON، WindRanger و ParmeSan به‌ ترتیب 0.86، 0.81، 0.83 و 0.89 به‌دست آمده است.

بر اساس تحلیل‌های فوق، می‌توان نتیجه گرفت که DeepGo قادر است سریع‌تر از فازرهای مبنا به نقاط هدف برسد.

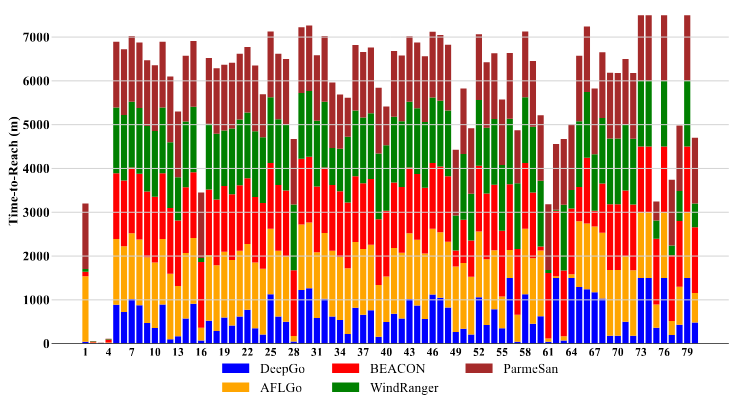
برای نمایش نتایج به صورت مستقیم، از نمودار میله‌ای استفاده کردیم. در شکل 5، محور افقی نشان‌دهندهٔ شناسهٔ نقاط هدف (1 تا 80) و محور عمودی نشان‌دهندهٔ کل زمان TTR همهٔ فازرها به دقیقه است، و هر میلهٔ کوتاه‌تر نشان‌دهندهٔ زمان کمتر برای رسیدن به هدف است.

چون برخی فازرها نمی‌توانند بعضی برنامه‌ها را کامپایل کنند یا در محدودهٔ زمانی 24 ساعت به نقاط هدف برسند، TTR برای این موارد ثبت نمی‌شود. برای تمایز این موارد، در شکل 5 مقدار 1500 دقیقه برای چنین نقاطی در نظر گرفته شده است.

از نمودار مشخص است که میله‌های آبی (DeepGo) به‌طور قابل توجهی کوتاه‌تر از سایر میله‌ها هستند، که نشان می‌دهد DeepGo می‌تواند بیشتر نقاط هدف را سریع‌تر از فازرهای مبنا پوشش دهد.

6.3 افشای آسیب‌پذیری‌ها

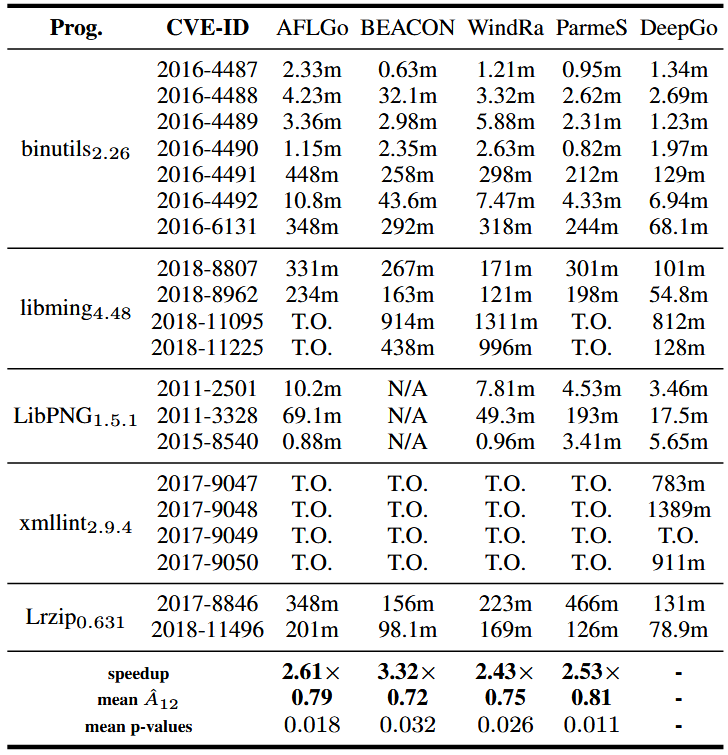
برای پاسخ به RQ2، همانند BEACON و WindRanger، از AFLGo testsuite استفاده کردیم و آسیب‌پذیری‌های شناخته‌شده با شناسه CVE در برنامه‌ها را به عنوان نقاط هدف مشخص کردیم. اطلاعات مربوط به نقاط هدف و نتایج TTE در جدول 1 ارائه شده است.

همان‌طور که جدول نشان می‌دهد، از میان 20 آسیب‌پذیری، DeepGo (19) بیشترین تعداد آسیب‌پذیری‌های کشف‌شده را نسبت به AFLGo (14)، BEACON (13)، WindRanger (16) و ParmeSan (14) دارد. علاوه بر این، در اکثر نقاط هدف (14 از 20)، DeepGo عملکرد بهتری نسبت به تمام فازرهای مبنا داشت و کمترین TTE را به دست آورد.

با توجه به میانگین TTE برای کشف آسیب‌پذیری‌ها، DeepGo به ترتیب ×2.61, ×3.32, ×2.43 و ×2.53 سریع‌تر از AFLGo، BEACON، WindRanger و ParmeSan عمل کرد. تمامی مقادیر P (p-valueها) کمتر از 0.05 بودند و میانگین A12ˆ نسبت به AFLGo، BEACON، WindRanger و ParmeSan برابر با 0.79، 0.72، 0.75 و 0.81 بود.

بر اساس تحلیل بالا، می‌توان نتیجه گرفت که DeepGo می‌تواند آسیب‌ پذیری‌های شناخته‌شده را سریع‌تر از فازرهای پایه‌ای (baseline fuzzers) آشکار کند.

6.4 اثربخشی VEE

برای پاسخ به سوال پژوهشی ۳ (RQ3)، پیش‌بینی‌های انجام‌ شده توسط VEE را در زمانی که DeepGo تعداد 20 برنامه از مجموعه UniBench را آزمایش می‌کرد، تحلیل کردیم. برای هر ورودی (pt, at)، VEE خروجی‌های (pt+1, rt) را با احتمال‌ها و پاداش‌های متفاوت (یعنی احتمال‌های پیش‌بینی‌شده و پاداش‌های پیش‌بینی‌شده) ارائه می‌دهد.

فازر همزمان، در طول فرآیند فازینگ، با اعمال اقدام at در مسیر pt باعث انتقال مسیرها با احتمال‌ها و پاداش‌های متفاوت می‌شود (یعنی احتمال‌ها و پاداش‌های واقعی). برای تحلیل دقت پیش‌بینی‌های VEE، معیار دقت (Accuracy) را به‌صورت زیر تعریف کردیم:

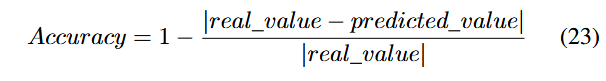
مقدار واقعی (real value) نشان‌دهنده‌ی احتمال واقعی یا پاداش واقعی و مقدار پیش‌بینی ‌شده (predicted value) نشان‌دهنده‌ی احتمال یا پاداش پیش‌بینی‌شده است. مقدار بالاتر دقت (Accuracy) نشان‌دهنده‌ی صحت بالاتر پیش‌بینی‌ها است.

در طول آزمایش هر برنامه از UniBench، دو نوع دقت هر انتقال مسیر هر ۳۰ دقیقه یکبار محاسبه شد. از آنجا که DeepGo آزمایش ۲۰ برنامه را پنج بار تکرار کرد، در هر نقطه زمانی، میانگین دقت احتمال پیش‌بینی‌شده (AAPP) و میانگین دقت پاداش پیش‌بینی‌شده (AAPR) تمام انتقال‌های مسیر تمام برنامه‌ها بر اساس معادله‌ی (23) محاسبه شد تا دقت پیش‌بینی‌های VEE ارزیابی شود.

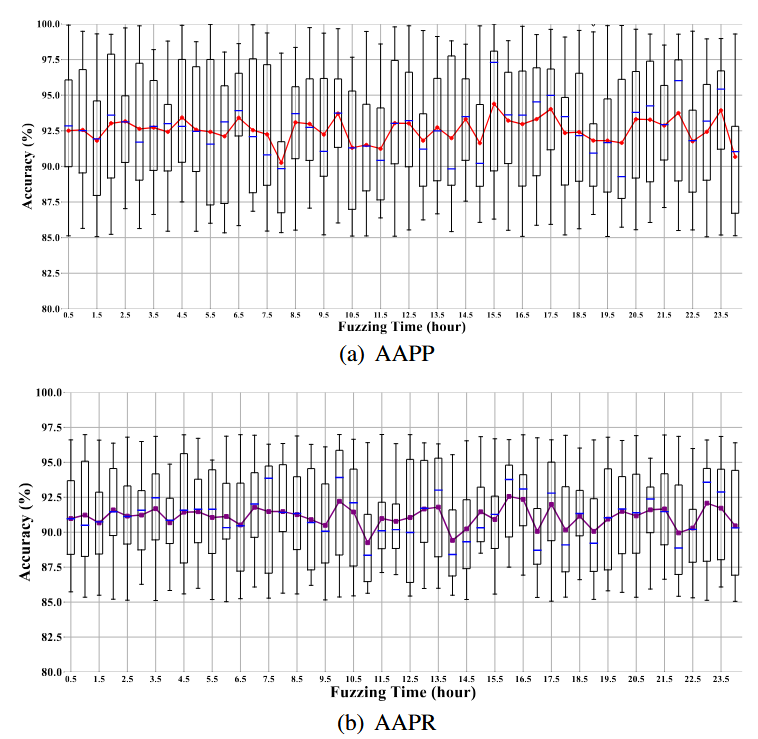
برای نمایش ساده و قابل فهم نتایج، از نمودار خطی استفاده شد. در شکل ۶، محور افقی نشان‌دهنده‌ی زمان fuzzing (از ۰ ساعت تا ۲۴ ساعت) و محور عمودی نشان‌دهنده‌ی دقت‌های AAPP و AAPR است که هر دو در بازه‌ی [0, 1] قرار دارند. همان‌طور که در شکل ۶ مشاهده می‌شود، از ۰.۵ ساعت تا ۲۴ ساعت، دقت‌های AAPP و AAPR همگی بالاتر از ۸۰٪ هستند و میانگین دقت‌های AAPP و AAPR در ۴۸ نقطه‌ی زمانی به ترتیب برابر با ۹۲.۵۷٪ و ۹۱.۱۰٪ است.

همچنین، برای نمایش دقت‌ها در برنامه‌های مختلف و در نقاط زمانی متفاوت از نمودارهای جعبه‌ای (box charts) استفاده شد. خط آبی نمایانگر میانه (median) و طول جعبه نشان‌دهنده‌ی بازه‌ی توزیع داده‌ها است. از این نمودارها مشاهده می‌شود که دقت‌های AAPP و AAPR در میان برنامه‌های مختلف تغییر قابل توجهی ندارند (≤ ۱۵٪) و در هر نقطه زمانی مقدار بالایی (≥ ۸۰٪) حفظ می‌کنند.

این نتایج نشان می‌دهد که VEE قادر است انحراف را هنگام شبیه‌سازی مدل انتقال مسیر محدود کند و احتمال‌ها و پاداش‌های انتقال مسیر را با دقت بالا پیش‌بینی نماید.

6.5 اثربخشی مدل RLF و مؤلفه FO

برای پاسخ به سوال پژوهشی ۴ (RQ4)، پاداش‌های انتقال مسیرهایی که در طول فرآیند فازینگ رخ داده بودند، جمع‌آوری شد تا میانگین پاداش انتقال مسیرها در دنباله‌ی انتقال مسیرها محاسبه شود. این کار نشان می‌دهد که آیا مدل RLF و مؤلفه FO می‌توانند فازر را هدایت کنند تا دنباله‌های بهینه‌ی انتقال مسیر با پاداش‌های بالاتر را اجرا نماید یا خیر.

از آنجا که بهینه‌سازی‌های DeepGo روی استراتژی‌های فازینگ مبتنی بر مدل RLF و مؤلفه FO هستند، حذف هر یک از آن‌ها باعث بی‌اثر شدن این بهینه‌سازی‌ها می‌شود. بنابراین، هر دو مؤلفه حذف شدند و یک فازر جدید به نام DeepGo-r ایجاد شد. ما از DeepGo و DeepGo-r برای آزمایش ۲۰ برنامه از مجموعه UniBench استفاده کردیم و پاداش تمام انتقال‌های مسیر برای تمام برنامه‌ها را هر ۳۰ دقیقه محاسبه کردیم. سپس در هر نقطه زمانی، میانگین پاداش (AR) برای ۲۰ برنامه محاسبه شد.

برای نمایش مستقیم نتایج، از نمودار خطی استفاده شد. در شکل ۷، محور افقی نشان‌دهنده‌ی زمان فازینگ (از ۰.۵ ساعت تا ۲۴ ساعت) و محور عمودی نشان‌دهنده‌ی مقادیر AR است، که در بازه‌ی [1-, 1-] قرار دارد.

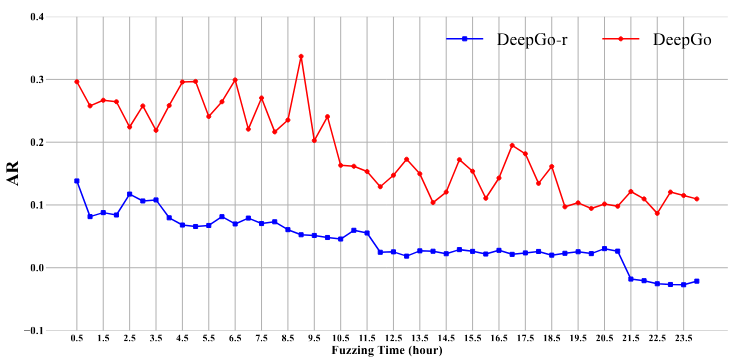
همان‌طور که در شکل ۷ مشاهده می‌شود، از ۰.۵ ساعت تا ۲۴ ساعت، روند کلی AR نزولی است که با این واقعیت هم‌خوانی دارد که با پیشرفت فرآیند فازینگ، یافتن بذرهای (seed) جدید برای فازر دشوارتر می‌شود.

میانگین پاداش AR برای DeepGo به‌طور قابل توجهی بالاتر از DeepGo-r بود؛ در هر نقطه زمانی، میانگین AR DeepGo تقریباً ۴.۲۶ برابر AR DeepGo-r بود. این امر نشان می‌دهد که مدل RLF و مؤلفه FO می‌توانند فازر را هدایت کنند تا دنباله‌های بهینه‌ی انتقال مسیر را اجرا نموده و سریع‌تر به سایت هدف برسد.

6.6 مطالعه‌ی حذف مؤلفه‌ها (Ablation Study)

برای پاسخ به سوال پژوهشی ۵، مطالعه‌ی حذف مؤلفه‌ها انجام شد تا تأثیر VEE، مدل RLF و مؤلفه FO بر عملکرد DeepGo بررسی شود. برای نشان دادن این که VEE، مدل RLF و مؤلفه FO می‌توانند جهت‌دهی (directedness) را بهبود بخشند، VEE از DeepGo حذف شد و یک ابزار جدید به نام DeepGo-v ایجاد شد. سپس آزمایش TTR با استفاده از DeepGo-v و DeepGo-r بر روی مجموعه UniBench انجام شد.

نتایج دقیق DeepGo-v و DeepGo-r در جدول 3 در ضمیمه ارائه شده است. بر اساس نتایج TTR، DeepGo توانست ۷۳ از ۸۰ سایت هدف را پیدا کند، در حالی که DeepGo-v ۳۲ از ۸۰ و DeepGo-r تنها ۱۸ از ۸۰ سایت هدف را رسیدند. علاوه بر این، DeepGo به ترتیب ۲.۰۵× و ۳.۷۲× بهتر از DeepGo-v و DeepGo-r در میانگین TTR برای رسیدن به سایت‌های هدف عمل کرد.

مقادیر p-value برابر با ۰.۰۱۳ و ۰.۰۰۶ و میانگین A12ˆ نسبت به DeepGo-v و DeepGo-r به ترتیب برابر با ۰.۸۳ و ۰.۹۰ بود. این نتایج نشان می‌دهند که VEE، مدل RLF و مؤلفه FO تأثیر قابل توجهی در کاهش TTR دارند.

ما همچنین از داده‌های میانی (intermediate data) استفاده می‌کنیم تا نشان دهیم DeepGo می‌تواند از مسیرهای غیرقابل اجرا و سخت پرهیز کند. ابتدا، یک seed را قابل دسترس (reachable seed یا Rseed) در نظر می‌گیریم اگر مسیر اجرایی آن حداقل یک بلوک پایه قابل دسترس را پوشش دهد (یعنی فاصله BB ≥ 0). ما میانگین تعداد Rseedهای تولیدشده توسط fuzzers مختلف هنگام آزمایش برنامه‌های مختلف و همچنین نسبت Rseedها (PRseed) نسبت به کل seedها را محاسبه می‌کنیم. اگر تعداد و نسبت Rseedها بیشتر باشد، نشان‌دهنده‌ی این است که fuzzer می‌تواند از صرف زمان بر مسیرهای غیرقابل اجرا و سخت پرهیز کند.

دوم، تعداد کل مسیرهایی که fuzzer برای رسیدن به سایت‌های هدف طی می‌کند (reached paths یا Rpath) را در طول آزمایش ۲۰ برنامه از UniBench اندازه‌گیری می‌کنیم. برای یک سایت هدف مشخص، مسیرهای مختلف می‌توانند نتایج آزمایشی متفاوتی ایجاد کنند. با شمارش تعداد کل Rpathها، می‌توان مشخص کرد که آیا DeepGo نسبت به سایر fuzzers می‌تواند مسیرهای بیشتری برای رسیدن به سایت هدف کشف کند یا خیر، و بنابراین امکان تست متنوع‌تر سایت هدف را فراهم می‌کند.

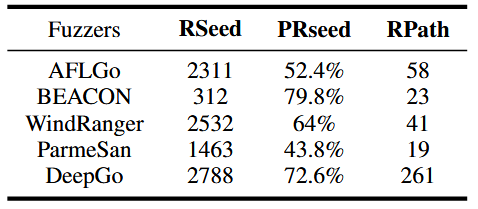
از نتایج جدول 2 می‌توان دو نتیجه گرفت:
۱. با مقایسه‌ی Rseed و Rpath تمام fuzzers، مشاهده می‌کنیم که DeepGo می‌تواند در همان بودجه زمانی Rseedهای بیشتری تولید کند.

۲. اگرچه BEACON دارای Rpath بالاتری است، اما به دلیل کوتاه کردن برخی مسیرهای قابل دسترس به سایت هدف، دارای کمترین Rseed در بین تمام fuzzers است.

DeepGo نیز علاوه بر BEACON، بالاترین نسبت Rseed (PRseed) را در بین تمام fuzzers دارد. این سه معیار میانی نشان می‌دهند که DeepGo می‌تواند مسیرهای بهینه و قابل اجرا به سایت هدف تولید کند، به‌طوری که از مسیرهای غیرقابل اجرا و سخت پرهیز می‌کند.

6.7 مطالعه‌ی موردی عملکرد DeepGo

برای نشان دادن اینکه چرا DeepGo می‌تواند سریع‌تر به نقاط هدف برسد، از نقطهٔ هدف get_audio.c:1605 در نسخهٔ lame3.99.5 به‌عنوان یک نمونه برای انجام مطالعهٔ موردی استفاده کردیم. همان‌طور که در لیست ۱ نشان داده شده است، خط ۲۴ به‌عنوان نقطهٔ هدف تعیین شده است. از آنجا که محدودیت‌های مسیر (path constraints) در خط ۲، خط ۱۶ و خط ۲۳ همگی محدودیت‌هایی هستند که برآورده کردن آن‌ها دشوار است، ابزارهای AFLGo و WindRanger نتوانستند در بازهٔ زمانی ۲۴ ساعته به نقطهٔ هدف برسند؛ در حالی که DeepGo در دقیقهٔ ۲۸۲ به نقطهٔ هدف (خط ۲۴) رسید.

در مورد AFLGo و WindRanger، ابزار AFLGo توانست به خطوط ۱۱–۱۲ برسد و WindRanger نیز توانست به خط ۱۷ برسد. با این حال، هیچ‌یک از آن‌ها نتوانستند محدودیت‌های مسیر در خطوط ۲، ۹–۱۰، ۱۶ و ۲۳ را به‌طور هم‌زمان برآورده کنند تا به نقطهٔ هدف برسند. نمونه‌ای از نقطهٔ هدف get_audio.c:1605 در نسخهٔ lame3.99.5 به شرح زیر است:

				
					int init_infile(){
	if (global.snd_file == 0) {
		global.music_in = open_wave_file(gfp, inPath);
	}
	else
		...
	}
	static FILE * open_wave_file(){
		if (global_reader.input_format != sf_raw &&
				(global_reader.input_format != sf_ogg){
			global_reader.input_format =
				parse_file_header(gfp,musicin);
		}
	}
	static int parse_file_header(){
		if (type == IFF_ID_FORM) {
			int const ret = parse_aiff_header(gfp, sf);
		}
		else
			...
	}
	static int parse_aiff_header(){
		if (dataType == IFF_ID_2CBE) {
			global.pcmswapbytes = !global_reader.swapbytes;
		}
		else
			...
	}

در نمونه کد بالا، شرط‌ها در مکان‌های مختلف کد با بایت‌های متفاوتی از seed مرتبط هستند (برای مثال، مقدار global.snd_file در خط ۲ و global_reader.input_format در خط ۱۱ توسط بایت‌های متفاوتی از seed تعیین می‌شوند) و تغییر دادن بایت‌های مرتبط باعث انتقال‌های متفاوت مسیر و دریافت پاداش‌های مختلف می‌شود. از آنجا که AFLGo و WindRanger قادر به پیش‌بینی انتقال‌های مسیر و میزان پاداش نیستند، نمی‌توانند از انجام اقداماتی که منجر به انتقال‌های کم‌پاداش می‌شوند اجتناب کنند. در نتیجه، بیشتر ورودی‌های جدید تولیدشده توسط AFLGo و WindRanger نتوانستند خطوط ۱۱–۱۲ و ۱۸ را پوشش دهند و بنابراین در رسیدن به نقطهٔ هدف (خط ۲۴) ناکام ماندند.

برای شناسایی چنین ارتباط‌هایی، در طول فرایند آزمون، ارتباط میان اقدام‌ها (بایت‌های جهش‌یافته یا mutation bytes) و انتقال‌های مسیر (path transitions) ثبت می‌شود. با جست‌وجوی مسیرهایی که شامل مکان‌های مشخصی از کد هستند، می‌توان اقدام‌های متناظر با آن‌ها را به دست آورد و در نتیجه، رابطهٔ متناظر میان مکان‌های کد و اقدام‌ها مشخص می‌شود.

به‌طور مشخص، DeepGo می‌تواند نگاشت‌های میان (مسیر، اقدام) یا (path, action) و (مسیر بعدی، پاداش) یا (next path, reward) را ثبت کند تا از آن‌ها برای آموزش VEE استفاده شود. اگر انتقال‌های مسیری که در اثر تغییر یک بایت خاص ایجاد می‌شوند بتوانند DeepGo را به پوشش مکان‌های مهم کد هدایت کنند (برای مثال، بخش‌هایی از کد که به نقاط هدف نزدیک‌تر هستند)، آن انتقال مسیر و اقدام متناظر با آن (یعنی بایت‌های جهش‌یافته) پاداش بالایی دریافت خواهند کرد.

با بررسی پاداش انتقال‌های مسیر مختلف، می‌توان تعیین کرد که برای رسیدن به مکان‌های مهم کد، کدام بایت‌ها باید دچار جهش (mutation) شوند.

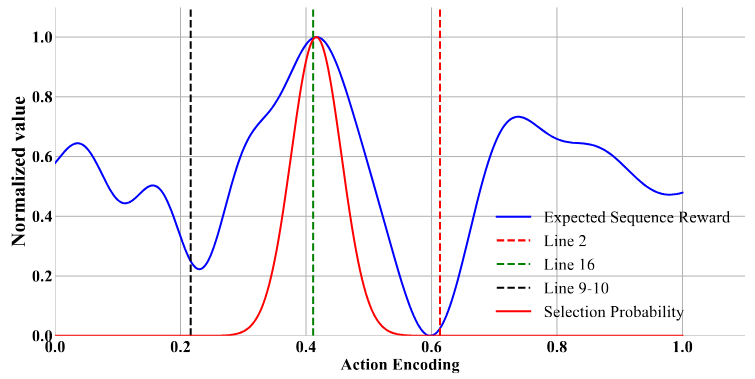
برای اثبات تحلیل فوق، ما پاداش مورد انتظار دنباله‌ای برای انجام همهٔ اقدام‌ها (یعنی جهش دادن تمام بایت‌ها) و همچنین احتمال انتخاب هر اقدام توسط RLF را پس از رسیدن DeepGo به خط ۱۲ محاسبه کردیم و نتایج را در شکل ۸ ارائه دادیم.

در شکل ۸، محور افقی (x) نشان‌دهندهٔ کدگذاری اقدام‌ها و محور عمودی (y) بیانگر مقدار نرمال‌سازی‌شدهٔ پاداش‌های مورد انتظار دنباله‌ای و احتمال‌های انتخاب اقدام‌ها است. خطوط ۲، ۹–۱۰ و ۱۶ به‌ترتیب نمایانگر سه اقدام با کدگذاری‌های 0.226، 0.41 و 0.618 هستند که بایت‌های مرتبط با شرط‌های محدودیتی در خطوط ۲، ۹–۱۰ و ۱۶ را تغییر می‌دهند.

خط آبی توزیع پاداش‌های مورد انتظار دنباله‌ای اقدام‌ها را نشان می‌دهد و خط قرمز توزیع احتمال گاوسی مدل RLF برای انتخاب اقدام‌ها را نمایش می‌دهد. همان‌طور که خط آبی نشان می‌دهد، مقادیر نرمال‌شدهٔ پاداش مورد انتظار برای این سه اقدام به‌ترتیب برابر با 0.232، 0.994 و 0.061 است. این بدان معناست که اگر فازر (fuzzer) اقدام‌های مربوط به خطوط ۲ و ۹–۱۰ را انجام دهد، انتقال‌های مسیر حاصل باعث می‌شود فازر از نقطهٔ هدف دورتر شود.

در مورد خط قرمز، احتمال‌های گاوسی برای خطوط ۲ و 9-10 تقریباً برابر صفر است، در حالی که این مقدار برای خط ۱۶ نزدیک به ۱ است. بنابراین، هنگام انتخاب اقدام‌ها با استفاده از نمونه‌برداری گاوسی، مدل RLF تمایل دارد اقدام‌های نزدیک به خط ۱۶ را انتخاب کند، نه اقدام‌های خطوط 2 و 9-10.

به این ترتیب، DeepGo با احتمال بالا اقدام‌هایی را انتخاب می‌کند که دارای پاداش مورد انتظار دنباله‌ای بالاتری هستند؛ موضوعی که به اجتناب از انتقال‌های مسیر کم‌پاداش — که فازر را از نقطهٔ هدف دور می‌کنند — کمک می‌کند.

7. بحث

7.1 تنظیم اَبَرپارامترها (Hyperparameters)

اَبَرپارامتر یا هایپرپارامترهای γ و k هر دو بر مقدار TTR در DeepGo تأثیر می‌گذارند. نخست، در فرایند آموزش مدل RLF، هایپرپارامتر γ برای ایجاد تعادل میان تأثیر پاداش‌های فعلی و پاداش‌های آینده بر مقدار انتقال (transition value) و پاداش‌های مورد انتظار دنباله‌ایِ حالت جاری و اقدام‌های آن استفاده می‌شود. اگر فقط بر پاداش‌های فعلی تمرکز شود، مدل RLF ممکن است در بهینه‌های محلی (local optima) گرفتار شود. در مقابل، اگر پاداش‌های آینده بیش از حد مورد تأکید قرار گیرند، ممکن است انتقال‌های مسیر با پاداش کم برای مسیر فعلی ایجاد شوند و در نتیجه کارایی هدایت ‌شده (directed efficiency) کاهش یابد. بنابراین، مقداردهی ابرپارامتر γ بر مقادیر Q، مقادیر V و سیاست (policy) مدل RLF اثر می‌گذارد و در نهایت TTR در DeepGo را تحت تأثیر قرار می‌دهد.

دوم، در راهبرد گسترش شاخه‌ای k-مرحله‌ای (k-step branch rollout)، هایپرپارامتر k برای تولید دنباله‌ای از انتقال‌های مسیر با طول k استفاده می‌شود. با افزایش مقدار k، مدل VEE می‌تواند انتقال‌های مسیر بیشتری را پیش‌بینی کند و این موضوع به RLF امکان می‌دهد در طراحی سیاست‌ها آینده‌نگری بیشتری داشته باشد. با این حال، مقدار بیش‌ازحد بزرگ برای k ممکن است دقت پیش‌بینی انتقال‌های مسیر و پاداش‌ها توسط VEE را کاهش دهد و در نتیجه سیاست RLF را به سمت دنباله‌های انتقال مسیر با پاداش پایین هدایت کند.

در نتیجه، تنظیم هایپرپارامترk هم بر دقت پیش‌بینی VEE و هم بر میزان آینده‌نگری سیاست RLF اثر گذاشته و در نهایت بر مقدار TTR در DeepGo تأثیر می‌گذارد.

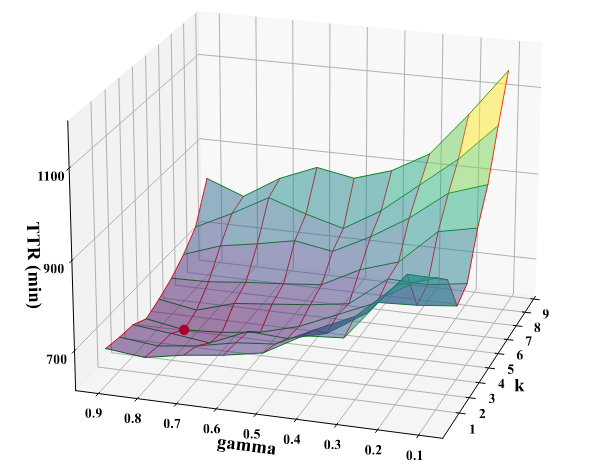
برای مشاهدهٔ تأثیر تغییر مقادیر γ و k بر عملکرد DeepGo، آزمایش‌هایی انجام دادیم که در آن مقدار γ برابر با 0.9، 0.8، 0.7، 0.6، 0.5، 0.4، 0.3، 0.2 و 0.1 و مقدار k برابر با 1 تا 9 تنظیم شد. سپس DeepGo با پیکربندی‌های مختلف هایپرپارامترها برای آزمون ۲۰ برنامه از UniBench مورد استفاده قرار گرفت و میانگین مقدار TTR برای هر مورد آزمایشی ثبت شد.

برای نمایش بصری تأثیر تنظیمات γ و k بر TTR در DeepGo، از یک نمودار سه‌بعدی استفاده کردیم که تغییرات TTR را با تغییر این دو پارامتر نشان می‌دهد. بر اساس شکل ۹، می‌توان سه نتیجهٔ اصلی گرفت:

کمترین مقدار TTR زمانی به دست می‌آید که γ برابر با 0.8 و k برابر با 4 تنظیم شود؛ این نقطه در شکل با یک نقطهٔ قرمز مشخص شده است.
اگر مقدار γ در بازه [0.5, 0.9] و مقدار k در بازه [3, 5] باشد، تنظیم این دو پارامتر تأثیر نسبتاً کمی بر TTR دارد (به‌طوری‌که TTR در بازه [648, 688] تغییر می‌کند).
مقدار TTR زمانی که γ بزرگ‌تر از 0.5 است، کمتر (بهتر) از حالتی است که γ کوچک‌تر از 0.5 باشد؛ همچنین وقتی k کمتر از 5 است، TTR نسبت به زمانی که k بزرگ‌تر از 5 باشد، کمتر است.

این نتایج نشان می‌دهد که با توجه به اطلاعات آماری فرایند fuzzing (که در آن طول دنباله‌های انتقال مسیر معمولاً کمتر از ۲۰ است) باید توجه بیشتری به تأثیر پاداش‌های فعلی مسیر داشت. علاوه بر این، مقدار k باید به‌گونه‌ای تنظیم شود که میان دقت پیش‌بینی و توان آینده‌نگری تعادل مناسبی برقرار گردد.

7.2 انتخاب اهداف (Selection of targets)

هنگام انتخاب اهداف برای ارزیابی، ابزار ++AFL را به مدت ۴۸ ساعت اجرا کردیم؛ زیرا معتقدیم تکنیک‌های فازینگ هدایت ‌شده (DGF) می‌توانند نسبت به تکنیک‌های فازینگ کلاسیک (CGF) سریع‌تر به اهداف از پیش تعیین‌شده برسند [23]، [39]، [86]، [88]. بنابراین، حتی اگر برخی اهداف توسط CGF در بازه‌ای بیشتر از ۲۴ ساعت اما کمتر از ۴۸ ساعت پوشش داده شوند، احتمال زیادی وجود دارد که روش‌های DGF بتوانند همان اهداف را در کمتر از ۲۴ ساعت پوشش دهند.

برای نمونه، در ارزیابی‌های ما، از میان ۵۱ هدفی که رسیدن به آن‌ها برای ++AFL بیش از ۲۴ ساعت زمان برد، تعداد ۴۵ هدف توسط یک یا چند فازر هدایت‌شده در کمتر از ۲۴ ساعت پوشش داده شدند.

ما از ++AFL به‌جای نسخهٔ «معمولی» AFL برای تعیین اهداف استفاده کردیم، زیرا ++AFL نتایج جامع‌تری ارائه می‌دهد و امکان ثبت دقیق زمان موردنیاز برای رسیدن روش‌های CGF به اهداف مختلف را فراهم می‌کند. با اطلاعاتی که ++AFL فراهم می‌کند، می‌توانیم مکان‌های کد و هزینهٔ زمانی لازم برای رسیدن به آن‌ها را بازتولید کنیم؛ موضوعی که برای انتخاب اهداف ضروری است. در مقابل، AFL چنین اطلاعات دقیقی را ارائه نمی‌دهد.

8. کارهای مرتبط (RELATED WORK)

8.1 اجرای نمادین هدایت ‌شده (Directed Symbolic Execution — DSE)

اجرای نمادین هدایت ‌شده (DSE) عمدتاً برای رسیدن به نقاط هدف به موتورهای اجرای نمادین مانند KLEE [13] ،KATCH [52] و BugRedux [5] متکی است. با استفاده از تحلیل برنامه و حل محدودیت‌ها (constraint solving)، روش DSE می‌تواند ورودی‌هایی تولید کند که به‌طور مؤثر از میان محدودیت‌های مسیر عبور کرده و به نقاط هدف برسند.

با وجود اینکه برخی پژوهش‌های پیشرفته مانند symcc [63]، symqemu [62] و JigSaw [16] برای بهبود اجرای نمادین پیشنهاد شده‌اند، همچنان تحلیل سنگین برنامه، مشکل انفجار مسیرها (path-explosion) و هزینهٔ بالای حل محدودیت‌ها باعث می‌شوند مقیاس‌پذیری DSE محدود باقی بماند.

8.2 فازینگ جعبه خاکستری هدایت ‌شده (Directed Grey-box Fuzzing — DGF)

فازینگ خاکستری هدایت ‌شده (DGF)، فاصله میان بذرها (seed) و اهداف از پیش تعیین‌شده را محاسبه می‌کند تا seedهای نزدیک‌تر به اهداف در اولویت قرار گیرند. به این ترتیب، مسئلهٔ دستیابی به هدف به‌صورت یک مسئله بهینه‌سازی تعریف می‌شود که هدف آن کمینه کردن فاصله میان seedها و اهدافشان است.

بر اساس ایدهٔ AFLGo، ابزارهایی مانند Hawkeye [15]، LOLLY [46]، Berry [44]، UAFL [78] و CAFL [40] معیارهای جدیدی مانند شباهت مسیر (trace similarity) و شباهت دنباله‌ای (sequence similarity) پیشنهاد دادند تا قابلیت هدایت فازر افزایش یافته و آسیب‌پذیری‌های سخت برای آشکارسازی شناسایی شوند. ابزار FuzzGuard [93] seedهای غیرقابل دسترسی را فیلتر می‌کند و BEACON [31] مسیرهای غیرممکن را هرس می‌کند؛ هر دو روش، کارآمدی DGF را بهبود می‌دهند.

M C2 سپس [67] DGF را به‌صورت یک مسئله جست‌وجوی راهنمای اوراکل (oracle-guided search) مدل‌سازی می‌کند تا ورودی‌ای پیدا شود که به هدف برسد و بدین ترتیب سرعت دستیابی به اهداف افزایش یابد. FISHFUZZ [92] امکان می‌دهد فازرها بین هزاران هدف به‌طور روان مقیاس‌پذیر عمل کنند و seedها را به مکان‌های مهم هدایت کنند تا تست برنامه جامع‌تر شود. ابزارهایی مانند SemFuzz [22], [85] از اطلاعات جریان داده و معنایی برای تولید ورودی‌های معتبر استفاده می‌کنند.

ابزارهایی مانند Parmesan [58]، V-Fuzz [58] و SAVIOR [19] از sanitizerها (مانند ASAN [66] و UBSan [47]) برای علامت‌گذاری کدهای احتمالی دارای باگ به‌عنوان نقاط هدف استفاده کرده و DGF را برای تست این نقاط هدایت می‌کنند. Hydiff [38]، SAVIOR [19] و Badger [55] seedهایی را که ممکن است باعث باگ‌های خاص شوند، اولویت می‌دهند و سپس اجرای نمادین (symbolic execution) بذرهای (seed) قابل دسترسی از چندین نقطه هدف را در اولویت قرار می‌دهند. ابزارهایی مانند DrillerGO [36] و Berry [44] دقت DSE و مقیاس‌پذیری DGF را ترکیب می‌کنند تا نقاط ضعف هرکدام را کاهش دهند.

با این حال، DGF هنوز از مشکل عبور از محدودیت‌های مسیر که برآورده کردن آنها دشوار است، رنج می‌برد. DeepGo با پیش‌بینی اطلاعات حیاتی اجرای برنامه و تعیین مسیر بهینه، با ترکیب اطلاعات تاریخی اجرای برنامه و اطلاعات پیش‌بینی‌شدهٔ آینده، می‌تواند مسیر بهینه و عملیاتی برای رسیدن به نقطه هدف تولید کند. با اجتناب از مسیرهای غیرممکن و سخت برای اجرا، فازر می‌تواند به نقاط هدف با دقت و کارایی بالاتر برسد.

8.3 فازینگ جعبه خاکستری مبتنی بر هوش مصنوعی (AI-Based Grey-box Fuzzing)

فازینگ جعبه خاکستری مبتنی بر هوش مصنوعی در کارهای پیشرفتهٔ قبلی [26]، [69]، [73]، [76]، [79]، [93] از تکنیک‌های هوش مصنوعی برای تقویت فازینگ جعبه خاکستری استفاده شده است. در میان این کارها، NEUZZ [69] و MTFUZZ [68] از روش‌های مبتنی بر گرادیان نزولی (gradient-descent) به منظور افزایش کارایی فازینگ هدایت ‌شده توسط پوشش (coverage-guided grey-box fuzzing) استفاده می‌کنند و رفتار شاخه‌ای گسسته برنامه تحت آزمایش (PUT) را تقریب می‌زنند.

ابزار AthenaTest [76] با استفاده از شبکه‌های محلی مبتنی بر ترنسفورمر (local transformer-based networks) ویژگی‌های بذرها (seed) را از مجموعه داده استخراج کرده و تست کیس‌ها را تولید می‌کند. ابزارهای DYNFuzz [91] و FuzzGuard [93] مدل‌هایی مبتنی بر شبکه‌های عصبی می‌سازند تا پیش‌بینی کنند که آیا بذرها (seed) به نقاط هدف دسترسی دارند یا خیر و بذرهای (seed) غیرقابل دسترسی را فیلتر می‌کنند تا هدایت ‌شدگی فازر افزایش یابد.

با این حال، تکنیک‌های موجود فازینگ خاکستری مبتنی بر هوش مصنوعی تنها بر انتخاب بایت‌های جهش‌یافته یا بذرها (seed) بهینه‌سازی انجام می‌دهند و نمی‌توانند تمام استراتژی‌های فازینگ را به‌طور جامع بهینه کنند. این محدودیت باعث می‌شود فازر در تولید مسیرهای بهینه برای رسیدن به نقاط هدف کمتر هوشمند عمل کند.

9. نتیجه‌گیری

در این مقاله، ما DeepGo را معرفی کردیم؛ یک فازر جعبه خاکستری هدایت ‌شده پیش‌بینی‌کننده (predictive directed greybox fuzzer) که می‌تواند با ترکیب اطلاعات تاریخی و پیش‌بینی‌شده، مسیر بهینه‌ای برای رسیدن به نقطه هدف در DGF فراهم کند.

DeepGo محیط ترکیبی مجازی (Virtual Ensemble Environment — VEE) را ایجاد می‌کند که با استفاده از شبکه‌های عصبی عمیق (DNNs) مدل انتقال مسیر را شبیه‌سازی کرده و پاداش‌های احتمالی برای انتقال‌های مسیر بالقوه را پیش‌بینی می‌کند. DeepGo با استفاده از مدل RLF، انتقال‌های مسیر تاریخی و پیش‌بینی‌شده را ترکیب کرده و دنبالهٔ انتقال مسیر با بالاترین پاداش دنباله‌ای را برای تولید مسیرهای بهینه تعیین می‌کند. DeepGo بر اساس الگوریتم MPSO، گروه اقدام‌ها (Action) را بهینه کرده و دنبالهٔ انتقال مسیر با پاداش بالا را اجرا می‌کند تا مسیر بهینه تحقق یابد.

DeepGo بر روی ۱۰۰ نقطه هدف در ۲۵ برنامه واقعی از ۲ مجموعه داده ارزیابی شد. نتایج آزمایش‌ها نشان می‌دهد که DeepGo در رسیدن به نقاط هدف و افشای آسیب‌پذیری‌های شناخته ‌شده از فازرهای هدایت ‌شده پیشرفته مانند AFLGo، BEACON، WindRanger و ParmeSan بهتر عمل می‌کند. علاوه بر این، DeepGo دقت بالایی در پیش‌بینی انتقال‌های مسیر که هنوز طی نشده‌اند نیز نشان می‌دهد.

تقدیر و سپاس‌گزاری (ACKNOWLEDGMENT)

این پژوهش به‌طور جزئی توسط برنامهٔ ملی تحقیق و توسعه کلیدی چین تحت گرنت شماره 2021YFB0300101، پروژه‌های تحقیقاتی دانشگاه ملی فناوری دفاع (ZK20-17, ZK20-09, ZK23-14)، بنیاد ملی علوم طبیعی چین (62272472, 61902405, U22B2005, 61972412, 62306328)، بنیاد علوم طبیعی استان Hunan (2021JJ40692) و برنامهٔ ملی پرسنل سطح بالا برای فناوری دفاع (2017-JCJQ-ZQ-013) حمایت شده است.

منابع

				
					[1] (2023) Gnu binutils. [Online]. Available: https://www.gnu.org/software/binutils/.. 
[2] (2023) Undefined behavior sanitizer - clang 9 documentation. http://clang.llvm.org/docs/UndefinedBehaviorSanitizer.
[3] C. Aschermann, S. Schumilo, T. Blazytko, R. Gawlik, and T. Holz, “REDQUEEN: fuzzing with input-to-state correspondence,” in 26th Annual Network and Distributed System Security Symposium, NDSS 2019, San Diego, California, USA, February 24-27, 2019. The Internet Society, 2019. [Online]. Available: https://www.ndss-symposium.org/ndss-paper/redqueen-fuzzing-with-input-to-state-correspondence/
[4] P. Auer, N. Cesa-Bianchi, Y. Freund, and R. E. Schapire, “The non-stochastic multiarmed bandit problem,” SIAM Journal on Computing, vol. 32, no. 1, pp. 48–77, 2002.
[5] P. Auer, N. Cesa-Bianchi, Y. Freund, and R. E. Schapire, “Gambling in a rigged casino: The adversarial multi-armed bandit problem,” Electron. Colloquium Comput. Complex., no. 68, 2000.
[6] L. A. Baxter, “Markov decision processes: Discrete stochastic dynamic programming,” Technometrics, vol. 37, no. 3, pp. 353–353, 1995.
[7] R. Bellman, “A markovian decision process,” Indiana University Mathematics Journal, vol. 6, no. 4, p. 15, 1957.
[8] A. A. S. W. Blair, W. Mambretti and M. Egele, “Hotfuzz: Discovering algorithmic denial-of-service vulnerabilities through guided microfuzzing,” Network and Distributed System Security Symposium, 2020.
[9] M. BoHme, V. T. Pham, M. D. Nguyen, and A. Roychoudhury, “Directed greybox fuzzing,” in Acm Sigsac Conference on Computer & Communications Security, 2017, pp. 2329–2344. 
[10] M. B¨ohme, V. Pham, and A. Roychoudhury, “Coverage-based greybox fuzzing as markov chain,” in Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, October 24-28, 2016. ACM, 2016, pp. 1032–1043.
[11] S. Bubeck and N. Cesa-Bianchi, “Regret analysis of stochastic and nonstochastic multi-armed bandit problems,” Found. Trends Mach. Learn., vol. 5, no. 1, pp. 1–122, 2012. [Online]. Available: https://doi.org/10.1561/2200000024
[12] M. B¨ohme. (2023) Directed greybox fuzzing with afl. https://github.com/ aflgo/aflgo.
[13] C. Cadar, D. Dunbar, and D. R. Engler, “KLEE: unassisted and automatic generation of high-coverage tests for complex systems programs,” in 8th USENIX Symposium on Operating Systems Design and Implementation, OSDI 2008, December 8-10, 2008, San Diego, California, USA, Proceedings. USENIX Association, 2008, pp. 209–224. 
[14] H. Chen, S. Guo, Y. Xue, Y. Sui, C. Zhang, Y. Li, H. Wang, and Y. Liu, “MUZZ: Thread-aware grey-box fuzzing for effective bug hunting in multithreaded programs,” in 29th USENIX Security Symposium (USENIX Security 20). USENIX Association, Aug. 2020, pp. 2325– 2342.
[15] H. Chen, Y. Xue, Y. Li, B. Chen, X. Xie, X. Wu, and Y. Liu, “Hawkeye: Towards a desired directed grey-box fuzzer,” in Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS 2018, Toronto, ON, Canada, October 15-19, 2018. ACM, 2018, pp. 2095–2108.
[16] J. Chen, J. Wang, C. Song, , and H. Yin, “Jigsaw: Efficient and scalable path constraints fuzzing,” in 43rd IEEE Symposium on Security and Privacy (Oakland’22), May 2022.
[17] P. Chen and H. Chen, “Angora: Efficient fuzzing by principled search,” in 2018 IEEE Symposium on Security and Privacy, SP 2018, Proceedings, 21-23 May 2018, San Francisco, California, USA. IEEE Computer Society, 2018, pp. 711–725. [Online]. Available: https://doi.org/10.1109/SP.2018.00046
[18] P. Chen, J. Liu, and H. Chen, “Matryoshka: Fuzzing deeply nested branches,” in Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, CCS 2019, London, UK, November 11-15, 2019. ACM, 2019, pp. 499–513.
[19] Y. Chen, P. Li, J. Xu, S. Guo, R. Zhou, Y. Zhang, T. Wei, and L. Lu, “SAVIOR: towards bug-driven hybrid testing,” in 2020 IEEE Symposium on Security and Privacy, SP 2020, San Francisco, CA, USA, May 18-21, 2020. IEEE, 2020, pp. 1580–1596.
[20] M. Cho, S. Kim, and T. Kwon, “Intriguer: Field-level constraint solving for hybrid fuzzing,” in Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, CCS 2019, London, UK, November 11-15, 2019, L. Cavallaro, J. Kinder, X. Wang, and J. Katz, Eds. ACM, 2019, pp. 515–530. [Online]. Available: https://doi.org/10.1145/3319535.3354249 
[21] K. Chua, R. Calandra, R. McAllister, and S. Levine, “Deep reinforcement learning in a handful of trials using probabilistic dynamics models,” in Advances in Neural Information Processing Systems, vol. 31, 2018.
[22] Z. Du, Y. Li, Y. Liu, and B. Mao, “Windranger: A directed greybox fuzzer driven by deviationbasic blocks,” in ICSE ’22: 44st International Conference on Software Engineering. ACM, 2022.
[23] A. Fioraldi, D. Maier, H. Eißfeldt, and M. Heuse, “AFL++ : Combining incremental steps of fuzzing research,” in 14th USENIX Workshop on Offensive Technologies (WOOT 20). USENIX Association, Aug. 2020.
[24] S. Gan, C. Zhang, P. Chen, B. Zhao, X. Qin, D. Wu, and Z. Chen, “GREYONE: Data flow sensitive fuzzing,” in 29th USENIX Security Symposium (USENIX Security 20). USENIX Association, Aug. 2020, pp. 2577–2594. [Online]. Available: https://www.usenix.org/conference/usenixsecurity20/presentation/gan
[25] V. Ganesh, T. Leek, and M. Rinard, “Taint-based directed whitebox fuzzing,” in 2009 IEEE 31st International Conference on Software Engineering, 2009, pp. 474–484.
[26] P. Godefroid, H. Peleg, and R. Singh, “Learn&fuzz: Machine learning for input fuzzing,” IEEE Computer Society, 2017.
[27] [Google. (2023) Ffmpeg and a thousand fixes. https://security.googleblog.com/ 2014/01/ffmpeg-and-thousand-fixes.html.
[28] T. Haarnoja, A. Zhou, P. Abbeel, and S. Levine, “Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor,” in Proceedings of the 35th International Conference on Machine Learning, 2018.
[29] H. v. Hasselt, A. Guez, and D. Silver, “Deep reinforcement learning with double q-learning,” in Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, ser. AAAI’16. AAAI Press, 2016, p. 2094–2100.
[30] L. Hongliang, Z. Yini, Y. Yue, X. Zhuosi, and J. Lin, “Sequence coverage directed greybox fuzzing,” in 2019 IEEE/ACM 27th International Conference on Program Comprehension (ICPC), 2019.
[31] H. Huang, Y. Guo, Q. Shi, P. Yao, R. Wu, and C. Zhang, “Beacon: Directed grey-box fuzzing with provable path pruning,” in The 43rd IEEE Symposium on Security and Privacy(S&P’22), May 2022.
[32] M. Janner, J. Fu, M. Zhang, and S. Levine, “When to trust your model: Model-based policy optimization,” in Advances in Neural Information Processing Systems, 2019.
[33] S. Jian, L. Cao, G. Pang, L. Kai, and G. Hang, “Embedding-based representation of categorical data by hierarchical value coupling learning,” in International Joint Conference on Artificial Intelligence, 2017.
[34] J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Icnn95- international Conference on Neural Networks, 1995.
[35] J. Kim and J. Yun, “Poster: Directed hybrid fuzzing on binary code,” in the 2019 ACM SIGSAC Conference, 2019.
[36] ——, “Poster: Directed hybrid fuzzing on binary code,” in the 2019 ACM SIGSAC Conference, 2019.
[37] I. A. Kunin, “Nonstationary processes,” Springer Berlin Heidelberg, 1982.
[38] T. Lattimore, “Regret analysis of the finite-horizon gittins index strategy for multi-armed bandits,” in Proceedings of the 29th Conference on Learning Theory, COLT 2016, New York, USA, June 23-26, 2016, ser. JMLR Workshop and Conference Proceedings, V. Feldman, A. Rakhlin, and O. Shamir, Eds., vol. 49. JMLR.org, 2016, pp. 1214–1245.
[39] lcamtuf. (2023) American fuzzy lop (afl) fuzzer. https://lcamtuf.coredump.cx/ afl/.
[40] G. Lee, W. Shim, and B. Lee, “Constraint-guided directed greybox fuzzing,” in 30th USENIX Security Symposium (USENIX Security 21). USENIX Association, Aug. 2021, pp. 3559–3576. [Online]. Available: https://www.usenix.org/conference/usenixsecurity21/presentation/lee-gwangmu 
[41] C. Lemieux and K. Sen, “Fairfuzz: a targeted mutation strategy for increasing greybox fuzz testing coverage,” in Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, ASE 2018, Montpellier, France, September 3-7, 2018. ACM, 2018, pp. 475–485. [Online]. Available: https://doi.org/10.1145/3238147.3238176
[42] X. Li, K. Wang, L. Liu, J. Xin, H. Yang, and C. Gao, “Application of the entropy weight and topsis method in safety evaluation of coal mines,” Procedia Engineering, vol. 26, pp. 2085–2091, 2011, iSMSSE2011. [Online]. Available: https://www.sciencedirect. com/science/article/pii/S1877705811052532
[43] Y. Li, S. Ji, Y. Chen, S. Liang, W. Lee, Y. Chen, C. Lyu, C. Wu, R. Beyah, P. Cheng, K. Lu, and T. Wang, “UNIFUZZ: A holistic and pragmatic metrics-driven platform for evaluating fuzzers,” in 30th USENIX Security Symposium, USENIX Security 2021, August 11-13, 2021. USENIX Association, 2021, pp. 2777–2794. [Online]. Available: https://www.usenix.org/conference/usenixsecurity21/presentation/li-yuwei
[44] H. Liang, L. Jiang, L. Ai, and J. Wei, “Sequence directed hybrid fuzzing,” in 27th IEEE International Conference on Software Analysis, Evolution and Reengineering, SANER 2020, London, ON, Canada, February 18-21, 2020. IEEE, 2020, pp. 127–137. [Online]. Available: https://doi.org/10.1109/SANER48275.2020.9054807
[45] H. Liang, Y. Zhang, Y. Yu, Z. Xie, and L. Jiang, “Sequence coverage directed greybox fuzzing,” ser. ICPC ’19. IEEE Press, 2019. [Online]. Available: https://doi.org/10.1109/ICPC.2019.00044
[46] ——, “Sequence coverage directed greybox fuzzing,” in 2019 IEEE/ACM 27th International Conference on Program Comprehension (ICPC), 2019, pp. 249–259. 
[47] LLVM/Clang. Clang 9 documentation c. undefined behavior sanitizer. http://clang.llvm.org/docs/UndefinedBehaviorSanitizer.html. 2023. 
[48] C. Lyu, S. Ji, C. Zhang, Y. Li, W. Lee, Y. Song, and R. A. Beyah, “Mopt: optimized mutation scheduling for fuzzers,” in USENIX Security Symposium, 2019.
[49] K. K. Ma, Y. P. Khoo, J. S. Foster, and M. Hicks, “Directed symbolic execution,” in Static Analysis - 18th International Symposium, SAS 2011, Venice, Italy, September 14-16, 2011. Proceedings, 2011.
[50] A. Mahendran and A. Vedaldi, “Understanding deep image representations by inverting them,” IEEE, 2015.
[51] P. D. Marinescu and C. Cadar, “KATCH: high-coverage testing of software patches,” in Joint Meeting of the European Software Engineering Conference and the ACM SIGSOFT Symposium on the Foundations of Software Engineering, ESEC/FSE’13, Saint Petersburg, Russian Federation, August 18-26, 2013. ACM, 2013, pp. 235–245. [Online]. Available: https://doi.org/10.1145/2491411.2491438 
[52] ——, “Katch: High-coverage testing of software patches,” in Proceedings of the 2013 9th Joint Meeting on Foundations of Software Engineering, ser. ESEC/FSE 2013. New York, NY, USA: Association for Computing Machinery, 2013, p. 235–245.
[53] V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra, and M. Riedmiller, “Playing atari with deep reinforcement learning,” 2013, nIPS Deep Learning Workshop 2013. 
[54] M. Nguyen, S. Bardin, R. Bonichon, R. Groz, and M. Lemerre, “Binary-level directed fuzzing for use-after-free vulnerabilities,” in 23rd International Symposium on Research in Attacks, Intrusions and Defenses, RAID 2020, San Sebastian, Spain, October 14-15, 2020. USENIX Association, 2020, pp. 47–62. [Online]. Available: https://www.usenix.org/conference/raid2020/presentation/nguyen
[55] Y. Noller, R. Kersten, and C. S. Pasareanu, “Badger: Complexity analysis with fuzzing and symbolic execution,” in Software Engineering and Software Management, SE/SWM 2019, Stuttgart, Germany, February 18-22, 2019, ser. LNI, S. Becker, I. Bogicevic, G. Herzwurm, and S. Wagner, Eds., vol. P-292. GI, 2019, pp. 65–66. [Online]. Available: https://doi.org/10.18420/se2019-16
[56] Y. Noller, C. S. Pasareanu, M. B¨ohme, Y. Sun, H. L. Nguyen, and L. Grunske, “Hydiff: hybrid differential software analysis,” in ICSE ’20: 42nd International Conference on Software Engineering, Seoul, South Korea, 27 June - 19 July, 2020, G. Rothermel and D. Bae, Eds. ACM, 2020, pp. 1273–1285. [Online]. Available:https://doi.org/10.1145/3377811.3380363
[57] S. ¨Osterlund, K. Razavi, H. Bos, and C. Giuffrida, “ParmeSan:Sanitizer-guided greybox fuzzing,” in 29th USENIX Security Symposium (USENIX Security 20). USENIX Association, 2020, pp.2289–2306. [Online]. Available: https://www.usenix.org/conference/ usenixsecurity20/presentation/osterlund
[58] ——, “ParmeSan: Sanitizer-guided greybox fuzzing,” in 29th USENIX Security Symposium (USENIX Security 20). USENIX Association, Aug. 2020, pp. 2289–2306. [Online]. Available: https://www.usenix. org/conference/usenixsecurity20/presentation/osterlund 
[59] J. Peng, F. Li, B. Liu, L. Xu, B. Liu, K. Chen, and W. Huo, “1dvul: Discovering 1-day vulnerabilities through binary patches,” in 49th Annual IEEE/IFIP International Conference on Dependable Systems and Networks, DSN 2019, Portland, OR, USA, June 24-27, 2019. IEEE, 2019, pp. 605–616. [Online]. Available:https://doi.org/10.1109/DSN.2019.00066
[60] ——, “1dvul: Discovering 1-day vulnerabilities through binary patches,” in 49th Annual IEEE/IFIP International Conference on Dependable Systems and Networks, DSN 2019, Portland, OR, USA, June 24-27, 2019. IEEE, 2019, pp. 605–616. [Online]. Available: https://doi.org/10.1109/DSN.2019.00066
[61] R. L. PLACKETT, “Studies in the history of probability and statistics: Vii. the principle of the arithmetic mean,” Biometrika, vol. 45, pp. 130–135, 1958. [Online]. Available: https://doi.org/10.1093/biomet/45. 1-2.130
[62] S. Poeplau and A. elien Francillon, “Symqemu: Compilation-based symbolic execution for binaries,” in 28th Annual Network and Distributed System Security Symposium, NDSS 2021, virtually, February 21-25, 2021. The Internet Society, 2021. [Online]. Available: https://www.ndss-symposium.org/ndss-paper/symqemu-compilation-based-symbolic-execution-for-binaries/
[63] S. Poeplau and A. Francillon, “Symbolic execution with symcc: Don’t interpret, compile!” in 29th USENIX Security Symposium, USENIX Security 2020, August 12-14, 2020, S. Capkun and F. Roesner, Eds. USENIX Association, 2020, pp. 181–198. [Online]. Available: https://www.usenix.org/conference/usenixsecurity20/presentation/poeplau
[64] M. Rajpal, W. Blum, and R. Singh, “Not all bytes are equal: Neural byte sieve for fuzzing,” 2017.
[65] T. Schaul, J. Quan, I. Antonoglou, and D. Silver, “Prioritized experience replay,” Computer Science, 2015.
[66] K. Serebryany, D. Bruening, A. Potapenko, and D. Vyukov, “AddressSanitizer: A fast address sanity checker,” in 2012 USENIX Annual Technical Conference (USENIX ATC 12). Boston, MA: USENIX Association, 2012, pp. 309–318. [Online]. Available: https://www.usenix.org/conference/atc12/technical-sessions/presentation/serebryany
[67] A. Shah, D. She, S. Sadhu, K. Singal, P. Coffman, and S. Jana, “Mc2: Rigorous and efficient directed greybox fuzzing,” ser. CCS ’22, Los Angeles, CA, USA, 2022. [Online]. Available: https://doi.org/10.1145/3548606.3560648
[68] D. She, R. Krishna, L. Yan, S. Jana, and B. Ray, “Mtfuzz: fuzzing with a multi-task neural network,” in ESEC/FSE ’20: 28th ACM Joint European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Virtual Event, USA, November 8-13, 2020. ACM, 2020, pp. 737–749. [Online]. Available: https://doi.org/10.1145/3368089.3409723
[69] D. She, K. Pei, D. Epstein, J. Yang, B. Ray, and S. Jana, “Neuzz: Efficient fuzzing with neural program smoothing,” in 2019 IEEE Symposium on Security and Privacy (SP), 2019, pp. 803–817.
[70] Y. Shi and R. Eberhart, “A modified particle swarm optimizer,” in 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat.No.98TH8360), 1998, pp. 69–73. 
[71] Y. Shin and L. Williams, “Can traditional fault prediction models be used for vulnerability prediction?” Empirical Software Engineering, vol. 18, no. 1, pp. 25–59, 2013.
[72] K. Simonyan, A. Vedaldi, and A. Zisserman, “Deep inside convolutional networks: Visualising image classification models and saliency maps,”Computer ence, 2013.
[73] S. Sivakorn, G. Argyros, K. Pei, A. D. Keromytis, and S. Jana, “Hvlearn: Automated black-box analysis of hostname verification in ssl/tls implementations,” in 2017 IEEE Symposium on Security and Privacy (SP), 2017. 
[74] N. Stephens, J. Grosen, C. Salls, A. Dutcher, R. Wang, J. Corbetta, Y. Shoshitaishvili, C. Kruegel, and G. Vigna, “Driller: Augmenting fuzzing through selective symbolic execution,” in 23rd Annual Network and Distributed System Security Symposium, NDSS 2016, San Diego, California, USA, February 21-24, 2016. The Internet Society, 2016. [Online]. Available: http://wp.internetsociety.org/ndss/wp-content/uploads/sites/25/2017/09/driller-augmenting-fuzzing-through-selective-symbolic-execution.pdf 
[75] Y. Sui and J. Xue, “SVF: interprocedural static value-flow analysis in LLVM,” in Proceedings of the 25th International Conference on Compiler Construction, CC 2016, Barcelona, Spain, March 12-18, 2016. ACM, 2016, pp. 265–266. [Online]. Available: https://doi.org/10.1145/2892208.2892235
[76] M. Tufano, D. Drain, A. Svyatkovskiy, S. K. Deng, and N. Sundaresan, “Unit test case generation with transformers and focal context,” arXiv, May 2021.
[77] H. Wang, X. Xie, Y. Li, C. Wen, Y. Li, Y. Liu, S. Qin, H. Chen, and Y. Sui, “Typestate-guided fuzzer for discovering use-after-free vulnerabilities,” in ICSE ’20: 42nd International Conference on Software Engineering, Seoul, South Korea, 27 June - 19 July, 2020. ACM, 2020, pp. 999–1010. [Online]. Available: https://doi.org/10.1145/3377811.3380386
[78] ——, “Typestate-guided fuzzer for discovering use-after-free vulnerabilities,” in ICSE ’20: 42nd International Conference on Software Engineering, Seoul, South Korea, 27 June - 19 July, 2020. ACM, 2020, pp. 999–1010. [Online]. Available: https://doi.org/10.1145/3377811.3380386 
[79] J. Wang, B. Chen, L. Wei, and Y. Liu, “Skyfire: Data-driven seed generation for fuzzing,” in The 38th IEEE Symposium on Security and Privacy(S&P’17). USENIX Association, 2017.
[80] X. Wang, J. Sun, Z. Chen, P. Zhang, J. Wang, and Y. Lin, “Towards optimal concolic testing,” in Proceedings of the 40th International Conference on Software Engineering, ICSE 2018, Gothenburg, Sweden, May 27 - June 03, 2018. ACM, 2018, pp. 291–302. [Online]. Available: https://doi.org/10.1145/3180155.3180177 
[81] Y. Wang, X. Jia, Y. Liu, K. Zeng, and P. Su, “Not all coverage measurements are equal: Fuzzing by coverage accounting for input prioritization,” in Network and Distributed System Security Symposium, 2020.
[82] C. Wen, H. Wang, Y. Li, S. Qin, Y. Liu, Z. Xu, H. Chen, X. Xie, G. Pu, and T. Liu, “Memlock: memory usage guided fuzzing,” in ICSE ’20: 42nd International Conference on Software Engineering, Seoul, South Korea, 27 June - 19 July, 2020. ACM, 2020, pp. 765–777. [Online]. Available: https://doi.org/10.1145/3377811.3380396
[83] M. Wu, L. Jiang, J. Xiang, Y. Huang, H. Cui, L. Zhang, and Y. Zhang, “One fuzzing strategy to rule them all,” in 44th IEEE/ACM 44th International Conference on Software Engineering, ICSE 2022, Pittsburgh, PA, USA, May 25-27, 2022. ACM, 2022, pp. 1634–1645. [Online]. Available: https://doi.org/10.1145/3510003.3510174
[84] Yang, Guowei, Rungta, Neha, Khurshid, Sarfraz, Person, and Suzette, “Directed incremental symbolic execution,” ACM SIGPLAN Notices: A Monthly Publication of the Special Interest Group on Programming Languages, 2011.
[85] W. You, P. Zong, K. Chen, X. Wang, X. Liao, P. Bian, and B. Liang, “Semfuzz: Semantics-based automatic generation of proof-of-concept exploits,” in Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS 2017, Dallas, TX, USA, October 30 - November 03, 2017. ACM, 2017, pp. 2139–2154.[Online]. Available: https://doi.org/10.1145/3133956.3134085
[86] T. Yue, P. Wang, Y. Tang, E. Wang, B. Yu, K. Lu, and X. Zhou, “EcoFuzz: Adaptive Energy-Saving greybox fuzzing as a variant of the adversarial Multi-Armed bandit,” in 29th USENIX Security Symposium (USENIX Security 20), 2020.
[87] I. Yun, S. Lee, M. Xu, Y. Jang, and T. Kim, “QSYM : A practical concolic execution engine tailored for hybrid fuzzing,” in 27th USENIX Security Symposium, USENIX Security 2018, Baltimore, MD, USA, August 15-17, 2018, W. Enck and A. P. Felt, Eds. USENIX Association, 2018, pp. 745–761. [Online]. Available:https://www.usenix.org/conference/usenixsecurity18/presentation/yun
[88] G. Zhang, P. Wang, T. Yue, X. Kong, S. Huang, X. Zhou, and K. Lu, “Mobfuzz: Adaptive multi-objective optimization in gray-box fuzzing,” 2022. [Online]. Available: https://api.semanticscholar.org/CorpusID:248224859.
[89] L. Zhao, Y. Duan, H. Yin, and J. Xuan, “Send hardest problems my way: Probabilistic path prioritization for hybrid fuzzing,” in 26th Annual Network and Distributed System Security Symposium, NDSS 2019, San Diego, California, USA, February 24-27, 2019. The Internet Society, 2019. [Online]. Available: https://www.ndss-symposium.org/ndss-paper/send-hardest-problems-my-way-probabilistic-path-prioritization-for-hybrid-fuzzing/
[90] Y. Zhao, Y. Li, T. Yang, and H. Xie, “Suzzer: A vulnerability guided fuzzer based on deep learning,” in Information Security and Cryptology - 15th International Conference, Inscrypt 2019, Nanjing, China, December 6-8, 2019, Revised Selected Papers, ser.Lecture Notes in Computer Science, Z. Liu and M. Yung, Eds., vol. 12020. Springer, 2019, pp. 134–153. [Online]. Available: https://doi.org/10.1007/978-3-030-42921-8 8 
[91] L. Zhaoji, W. Tianyuan, Z. Ziqiang, and et al., “Directed grey-box fuzzing technology based on lstm and dynamic strategy,” Computer Engineering and Applications, vol. 58, no. 18, pp. 147–153, 2022.
[92] H. Zheng, J. Zhang, Y. Huang, Z. Ren, H. Wang, and C. Cao, “Fishfuzz: Catch deeper bugs by throwing larger nets,” in 32th USENIX Security Symposium (USENIX Security 23). USENIX Association, Aug. 2023.
[93] P. Zong, T. Lv, D. Wang, Z. Deng, R. Liang, and K. Chen,“FuzzGuard: Filtering out unreachable inputs in directed grey-box fuzzing through deep learning,” in 29th USENIX Security Symposium (USENIX Security 20). USENIX Association, Aug. 2020, pp.2255–2269. [Online]. Available: https://www.usenix.org/conference/usenixsecurity20/presentation/zong

DeepGo: فازینگ جعبه خاکستری پیش‌بینانه و هدایت ‌شده

DeepGo: Predictive Directed Greybox Fuzzing