اجرای نمادین و آزمون برنامه ‌ها

این مقاله به اجرای نمادین (Symbolic Execution) برنامه ‌ها می‌ پردازد. به جای آنکه ورودی‌ های معمولی یک برنامه (مانند اعداد) ارائه شود، از نمادهایی استفاده می‌ شود که مقادیر دلخواه را نمایندگی می‌ کنند. اجرای برنامه همانند اجرای معمولی ادامه می ‌یابد، با این تفاوت که مقادیر می ‌توانند فرمول‌های نمادین بر پایه این نمادها باشند. مسائل پیچیده و در عین حال جالب، عمدتاً در هنگام اجرای نمادین دستورات شرطی و انشعابی به ‌وجود می‌ آیند.

در این مقاله همچنین یک سیستم خاص به نام EFFIGY معرفی شده است که اجرای نمادین را برای آزمون و دیباگ برنامه ‌ها فراهم می‌ کند. این سیستم برنامه ‌های نوشته شده به سبک ساده‌ ای از زبان برنامه نویسی PL/I را به صورت تفسیر شده اجرا می کند. این سیستم شامل بسیاری از قابلیت ‌های استاندارد دیباگینگ، توانایی مدیریت و اثبات ویژگی ‌ها در عبارات نمادین (symbolic expressions)، یک مدیر ساده برای آزمون برنامه ‌ها و یک برنامه ‌سنج برای صحت برنامه ‌ها می‌ باشد. همچنین، بحث مختصری درباره‌ رابطه بین اجرای نمادین و اثبات صحت برنامه ‌ها ارائه شده است.

واژگان کلیدی: اجرای نمادین، آزمون برنامه، دیباگ برنامه، اثبات برنامه، اعتبار سنجی برنامه، تفسیر نمادین

رده‌ بندی CR: 4.13, 5.21, 5.24

1. مقدمه

تولید گسترده برنامه ‌های قابل اعتماد، از بنیادی ‌ترین نیازها برای به ‌کارگیری رایانه ‌ها در حل مسائل پیچیده و چالش ‌برانگیز امروزی است. برای دستیابی به این هدف، روش ‌های گوناگونی در عمل مورد استفاده قرار می‌ گیرند و در عین حال، شماری از روش‌ های دیگر در کانون پژوهش ‌های کنونی قرار دارند.

پژوهشی که در این مقاله گزارش شده است، بر آن است تا اطمینان از انطباق برنامه با نیازمندی ‌های مورد نظر را فراهم آورد، حتی در شرایطی که مشخصات رسمی برنامه به ‌روشنی بیان نشده باشند. فناوری موجود در این حوزه، در اساس بر آزمون برنامه ‌ها استوار است. به بیان دیگر، نمونه ‌ای محدود از داده هایی که برنامه باید با آنها سروکار داشته باشد، در اختیار برنامه قرار می گیرد. اگر برنامه در پردازش این نمونه نتایج درست و مورد انتظار را تولید کند، فرض بر آن گذاشته می ‌شود که برنامه به ‌طور کلی صحیح عمل می‌کند. بخش عمده ‌ای از پژوهش‌ های جاری [11] بر این مسئله متمرکز است که چگونه باید این نمونه داده ‌ها را انتخاب کرد تا فرآیند آزمون بتواند بیشترین اطمینان را از درستی عملکرد برنامه فراهم آورد.

پژوهش ‌های اخیر در زمینه اثبات درستی برنامه ‌ها از طریق تحلیل رسمی (formal analysis) چشم‌ انداز بسیار امیدوار کننده ‌ای را نشان می ‌دهند و به ‌نظر میرسد این رویکرد بتواند در نهایت به عنوان روش نهایی برای تولید برنامه‌ های قابل اعتماد شناخته شود. با این حال، دستاوردهای عملی در این حوزه هنوز تا رسیدن به ابزاری که بتوان از آن در استفاده‌ های روزمره بهره گرفت، فاصله زیادی دارند. مشکلات بنیادی در تبدیل نظریه به عمل، بعید است در آینده نزدیک به ‌طور کامل برطرف شوند.

میتوان آزمون برنامه و اثبات برنامه را به ‌منزله دو سر یک طیف در نظر گرفت. در آزمون برنامه، برنامه ‌نویس می تواند با بررسی دقیق خروجی ‌ها اطمینان یابد که اجرای برنامه بر روی نمونه‌ داده ‌های آزمون به ‌درستی انجام می ‌شود. با این حال، درستی اجرای برنامه برای ورودی‌ هایی خارج از این مجموعه نمونه همچنان در ابهام باقی می ‌ماند.
در مقابل، در اثبات برنامه، برنامه ‌نویس به ‌صورت صوری نشان می ‌دهد که برنامه، مشخصات مورد نظر را در تمامی اجراها برآورده

می کند، بی ‌آنکه نیاز باشد برنامه واقعاً اجرا شود. برای انجام این کار، باید ابتدا رفتار صحیح برنامه به ‌طور دقیق مشخص گردد، سپس با پیروی از یک روند اثبات رسمی نشان داده شود که برنامه و مشخصات با یکدیگر سازگار هستند. اعتماد به این روش بستگی تام دارد به دقت و صحتی که در تدوین مشخصات و ساخت گام‌ های اثبات به کار می‌ رود، و نیز به میزان توجه به مسائل وابسته به ماشین مانند سرریز، گرد کردن اعداد و جزئیات مشابه.

این مقاله رویکردی میان‌ گرایانه و عملی را میان این دو سر طیف معرفی می ‌کند. از دیدگاهی ساده، این روش را می‌ توان گونه ‌ای آزمون پیشرفته دانست. در این شیوه، به جای اجرای برنامه بر روی مجموعه ‌ای از ورودی ‌های نمونه، برنامه به ‌صورت نمادین بر روی مجموعه ‌ای از کلاس ‌های ورودی اجرا می ‌شود. به بیان دیگر، هر اجرای نمادین می ‌تواند معادل با شمار زیادی از اجرای‌ های عادی در آزمون معمولی باشد. نتایج این اجرای نمادین را می‌ توان چه به ‌صورت رسمی و چه غیررسمی، با انتظارات برنامه ‌نویس از رفتار صحیح برنامه مقایسه و ارزیابی کرد.

دسته ورودی ‌هایی که هر اجرای نمادین نمایندگی می ‌کند، به وابستگی جریان کنترل برنامه به ورودی ‌ها بستگی دارد. اگر جریان کنترل برنامه کاملاً از متغیرهای ورودی مستقل باشد، یک اجرای نمادین برای بررسی تمام اجرای‌ های ممکن برنامه کفایت می کند. اما اگر جریان کنترل وابسته به ورودی ‌ها باشد، باید از تحلیل موردی استفاده کرد. در بسیاری از موارد، تعداد حالت ‌های ورودی لازم برای پوشش دادن تمامی حالات ممکن، از لحاظ نظری بی ‌نهایت است؛ از این ‌رو این روش همچنان در بنیاد خود نوعی آزمون محسوب می‌ شود.

با این حال، تفاوت اصلی در آن است که کلاس ‌های ورودی تنها بر اساس آن دسته از ورودی‌ هایی که در جریان کنترل برنامه موثرند تعیین می ‌شوند، و از این رو آزمون نمادین در اغلب برنامه ‌ها نویدبخش نتایجی دقیقتر و کارآمدتر از آزمون ‌های معمولی است.

2. اجرای نمادین (Symbolic Execution)

در این بخش اجرای نمادین یک برنامه به ‌صورت ایده آل توصیف می ‌شود و سپس در بخش ششم، سیستمی عملی که بر مبنای این مفهوم ساخته شده است و در واقع نسخه ‌ای نزدیک به وضعیت ایده ‌آل (approximation) به شمار می‌ آید ــ مورد بررسی قرار می گیرد.

واژه ایده آل در اینجا از چند جهت به ‌کار رفته است:

فرض بر این است که برنامه ‌ها تنها با اعداد صحیح سروکار دارند، و در واقع تنها با اعداد صحیحی که دارای اندازه دلخواه و نامحدود هستند. بنابراین، پدیده ‌هایی مانند سرریز ثبات ‌های ماشین در نظر گرفته نمیشوند.
درخت اجرا (یا execution tree که در ادامه تعریف خواهد شد) حاصل از اجرای نمادین بسیاری از برنامه ‌ها ــ و در واقع اکثر آن‌ ها بی‌ نهایت بزرگ است.
اجرای نمادین دستورات شرطی IF مستلزم اثبات قضایا (Theorem Proving) است، که حتی برای زبان ‌های برنامه ‌نویسی نسبتاً ساده نیز از نظر مکانیکی غیرممکن است.

با این ‌همه، بحث درباره حالت ایده‌ آل معیاری فراهم می ‌آورد که بر پایه آن می توان سامانه ‌های واقعی اجرای نمادین را در رایانه ‌ها سنجید و ارزیابی کرد.

هر زبان برنامه ‌نویسی دارای نوعی معنای اجرایی (execution semantics) است که مشخص می ‌کند متغیرهای برنامه چه نوع داده‌ هایی را می‌ توانند نمایش دهند، دستورات زبان چگونه این داده‌ ها را دست‌ کاری می کنند، و جریان کنترل چگونه میان دستورات مختلف برنامه پیش می ‌رود. در کنار این معناشناسی اجرایی، می ‌توان نوعی معناشناسی اجرای نمادین نیز برای زبان تعریف کرد؛ در این معناشناسی، داده ‌های واقعی مورد استفاده قرار نمی گیرند، بلکه به ‌جای آن‌ ها نمادهایی دلخواه به کار می‌ روند.
اجرای نمادین را می ‌توان گسترشی طبیعی از اجرای معمولی دانست، که اجرای واقعی را به‌ منزله حالتی خاص از خود دربر می‌ گیرد. در این روش، تعاریف محاسباتی عملگر های پایه زبان گسترش می ‌یابند تا بتوانند ورودی‌ های نمادین را بپذیرند و خروجی ‌هایی به صورت فرمول‌ های نمادین تولید کنند.

اکنون زبانی برنامه ‌نویسی ساده را در نظر بگیریم:
متغیرهای برنامه همگی از نوع عدد صحیح علامت ‌دار باشند. زبان شامل دستورات انتساب ساده، دستورات شرطی IF (به ‌همراه بندهای THEN و ELSE)، جهش‌ های GOTO به برچسب ‌ها، و نیز ساز و کاری برای دریافت ورودی‌ ها (مانند پارامترهای رویه ‌ای، متغیرهای سراسری، یا عملیات خواندن) است.
بیان ‌های حسابی در این زبان به عملگر های پایه اعداد صحیح یعنی جمع (+)، تفریق (–) و ضرب (×) محدود می‌ شوند.
بیان ‌های عبارت منطقی (که در دستورات IF به کار می‌ روند) نیز به آزمونی ساده از این نوع محدودند که آیا مقدار یک بیان حسابی نامنفی است یا نه ( برای نمونه {arith. expr. ≥ 0}).

اکنون می ‌توان اجرای نمادین برنامه ‌هایی را که به این زبان نوشته شده ‌اند توصیف کرد؛ بدین ترتیب که معنای اجرایی معمولی را به ‌عنوان پیش‌ فرض می ‌پذیریم و سپس آن را برای حالت نمادین اصلاح می کنیم. لازم به تأکید است که نه نحو (syntax) زبان و نه برنامه ‌هایی که در آن نوشته می شوند تغییر نمیکنند؛ تنها تفاوت در این است که در اجرای نمادین، داده ‌ها می توانند نمادین باشند.

تنها نقطه ‌ای که در آن داده ‌های نمادین (یعنی نمادهایی که نماینده اعداد صحیح هستند) وارد برنامه می ‌شوند، در ورودی ‌های برنامه است. برای سادگی فرض می کنیم هرگاه برنامه به مقدار ورودی تازه ‌ای نیاز داشته باشد، آن مقدار به ‌صورت نمادین از میان فهرستی از نمادها مانند { a₁ , a₂ , a₃ , … } تأمین می‌ شود. ورودی ‌های برنامه در نهایت به مقادیر متغیرهای برنامه تخصیص داده می ‌شوند (برای نمونه از طریق پارامترهای رویه، متغیرهای سراسری یا دستورات خواندن). بنابراین، برای پشتیبانی از ورودی های نمادین، لازم است اجازه دهیم که مقادیر متغیر ها بتوانند هم نمادهایی مانند aᵢ باشند و هم ثابت های عدد صحیح علامت دار.

قواعد ارزیابی برای عبارات حسابی که در دستورات انتساب (Assignment) و شرطی (IF) به کار می‌ روند، باید گسترش یابند تا بتوانند مقادیر نمادین را نیز پردازش کنند.

عباراتی که به شیوه معمول از ترکیب اعداد صحیح، مجموعه ای از نمادهای نامعین {a₁, a₂, …}، پرانتزها و عملگر های +، − و × ساخته میشوند، در واقع چند جمله‌ای های صحیح (دارای ضرایب صحیح و مقادیر صحیح) بر حسب آن نمادها هستند.

با اجازه دادن به متغیرهای برنامه برای آنکه بتوانند چند جمله‌ ای هایی بر حسب نمادهای aᵢ را به‌ عنوان مقدار بپذیرند، اجرای نمادین دستورات انتساب به‌ طور طبیعی قابل تعریف میشود. در این حالت، عبارت سمت راست دستور انتساب ارزیابی میشود و ممکن است در این فرایند، مقادیر متغیر ها با عبارات چند جمله ‌ای جایگزین گردند. حاصل این ارزیابی یک چند جمله ای خواهد بود (که در ساده ترین حالت می تواند یک عدد صحیح باشد) و سپس به عنوان مقدار جدید برای متغیر سمت چپ دستور انتساب در نظر گرفته می شود.

دستورات GOTO دقیقاً همانند اجرای عادی عمل می کنند، بدین معنا که کنترل برنامه را بدون قید و شرط از دستور GOTO به دستور دارای برچسب مربوطه منتقل می ‌سازند.

حالت (State) اجرای یک برنامه معمولاً شامل مقادیر متغیرهای برنامه و شمارنده دستورات (که مشخص می کند در حال حاضر کدام دستور در حال اجرا است) می ‌شود. اما در تعریف اجرای نمادین دستور IF، لازم است مؤلفه دیگری با عنوان شرط مسیر یا به اختصار pc نیز به حالت اجرا افزوده شود.

شرط مسیر یا pc، یک عبارت منطقی بر حسب ورودی های نمادین {aᵢ} است. این عبارت هرگز شامل متغیرهای برنامه نمیشود، و در زبان ساده ما، به ‌صورت ترکیب هم ‌بسته ‌ای (conjunction) از عبارات به شکل R ≥ 0یا ¬(R ≥ 0) در می‌ آید؛ که در آن R یک چند جمله ‌ای بر حسب نمادهای {aᵢ} است. برای نمونه:

{a₁ ≥ 0 ∧ a₁+2 * a₂ ≥ 0) ∧ ¬ (a₃ ≥ 0)}

همانطور که دیده خواهد شد، pc یا شرط مسیر (path condition) مجموعه‌ای از ویژگی ها و محدودیت‌ ها (properties) را جمع‌ آوری یا انباشت (accumulator) میکند و ورودی ها (inputs) باید این ویژگیها را برآورده کنند تا اجرای برنامه مسیر خاص مربوطه (associated path) را دنبال کند. هر اجرای نمادین (symbolic execution) با مقداردهی اولیه pc برابر با true آغاز میشود. هرگاه فرضیاتی درباره ورودی ها مطرح شود تا بتوان بین مسیرهای جایگزین برنامه، همان‌ طور که توسط دستورات IF ارائه شده است، انتخاب کرد، این فرضیات به pc افزوده میشوند. اجرای نمادین یک دستور IF به شکلی مشابه اجرای عادی آن آغاز می شود: ابتدا عبارت منطقی مرتبط ارزیابی می شود و متغیر ها با مقادیرشان جایگزین میشوند. از آنجایی که مقادیر متغیر ها چند جمله ای هایی بر مجموعه {a_i} هستند، در این شرط عبارتی به شکل زیر است: خواهد بود ، که در آن R یک چند جمله ‌ای است. چنین عبارتی را q بنامید. با استفاده از شرط مسیر فعلی pc، دو عبارت زیر را تشکیل دهید:

				
					(a)  pc ⊃ q
(b)  pc ⊃ ¬q

حداکثر یکی از این عبارات می تواند درست (true) باشد (با حذف حالت بدیهی که در آن pc به طور یکسان برابر با نادرست (false) است). زمانی که دقیقاً یک عبارت درست باشد، اجرای دستور IF همانند حالت عادی ادامه می یابد و کنترل برنامه به بخش THEN منتقل می شود، اگر عبارت (a) درست باشد، یا به بخش ELSE، اگر عبارت (b) درست باشد. تمام اجراهای عادی که مقادیر ورودیهایشان pc را برآورده میکند، همان مسیر جایگزین را دنبال خواهند کرد که این اجرای نمادین طی می کند؛ همه آنها یا بخش THEN را خواهند گرفت (pc ⊃ q) یا همه بخش ELSE را خواهند گرفت (pc ⊃ ¬q). در این حالت، اجرای دستور IF را «اجرای بدون انشعاب» (Non-forking execution) می نامند.

مورد جالب تر زمانی رخ می دهد که هیچ یک از عبارت های (a) و (b) درست (true) نباشند. در این وضعیت، حداقل یک مجموعه ورودی برای برنامه وجود دارد که pc را برآورده می کند و بخش THEN را انتخاب خواهد کرد و حداقل یک مجموعه ورودی دیگر وجود دارد که pc را برآورده می کند و به بخش ELSE هدایت خواهد شد. از آنجایی که هر دو مسیر جایگزین در این حالت ممکن هستند، تنها روش کامل، بررسی هر دو مسیر کنترل است. بنابراین، اجرای نمادین به گونه‌ ای تعریف می شود که به دو اجرای «موازی» تقسیم شود: یکی مسیر THEN و دیگری مسیر ELSE را دنبال می کند. هر دوی این اجراها حالت محاسباتی موجود دقیقاً قبل از اجرای دستور IF را فرض می کنند اما پس از آن به طور مستقل ادامه می یابند. در این حالت، اجرای دستور IF را «اجرای با انشعاب» (forking execution) می نامند. توجه داشته باشید که ویژگی انشعاب/عدم انشعاب (forking/non-forking characteristic) مربوط به یک اجرای خاص از دستور IF است و نه خود دستور؛ یک اجرای خاص از یک دستور IF ممکن است با انشعاب باشد، در حالی که اجرای بعدی همان دستور می تواند بدون انشعاب باشد.

از آنجا که در انتخاب مسیر THEN، فرض می شود ورودی ‌ها عبارت q (عبارت منطقی ارزیابی شده دستور IF) را برآورده می کنند، این اطلاعات در pc ثبت می شود با انجام انتساب (pc←pc ∧ q). به همین ترتیب، انتخاب مسیر ELSE منجر به (pc←pc ∧ ¬q) می شود. pc «شرط مسیر» (path condition) نامیده می شود زیرا جمع آوری شرایطی است که مسیر کنترل یکتا (unique control flow path) در برنامه را تعیین می کند. هر اجرای با انشعاب از دستور IF، یک شرط بر سمبل ها یا نمادهای ورودی (input symbols) ایجاد می کند که توسط انتخاب مسیر خاص تعیین می شود. pc برای اجراهای بدون انشعاب دستور IF تغییر نمیکند، زیرا هیچ فرض جدیدی ایجاد یا مورد نیاز نیست. pc هرگز نمیتواند نادرست (false) شود، زیرا مقدار اولیه آن درست (true) است و تنها عملیاتی که بر pc انجام میشود، عمل جمع است.

شکل 1. رویه SUM:

				
					SUM: PROCEDURE (A,B,C);
	X ← A + B;
	Y ← B + C;
	Z ← X + Y - B;
	RETURN (Z);
END;

یک دستور انتسابی به شکل:

pc ← pc ∧ r (که در آن r یا q یا not q است) اما فقط در حالتی که (pc ∧ r) برآورده باشد (pc ∧ r≡ ¬(pc ⊃ ¬r) که برآورده است اگر و تنها اگر if(pc ⊃ r) (قضیه نباشد)).

2.1 مثال‌ها

برنامه ساده ای که در شکل ۱ نشان داده شده است را در نظر بگیرید. این برنامه با نحو PL/I نوشته شده و مجموع سه مقدار را محاسبه می کند. در اجرای معمولی این برنامه، اگر ورودی ها اعداد صحیح ۱، ۳ و ۵ باشند، همانطور که در شکل ۲ نشان داده شده است، خروجی برنامه برابر با ۹ خواهد بود.

اجرای نمادین این برنامه که جزئیات آن در شکل ۳ آمده است، نشان می دهد که برای هر سه عدد صحیح دلخواه، مثلاً a₁, a₂, a₃، برنامه مجموع آنها را محاسبه خواهد کرد a₁+ a₂+ a₃.

حال برنامه ای کمی پیچیده تر را در شکل ۴ در نظر بگیرید که توان گیری عدد صحیح X به توان Y را انجام میدهد. اگر ورودی های نمادین a1 و a2 به ترتیب به عنوان مقادیر X و Y داده شوند، اجرای نمادین برنامه همانطور که در شکل ۵ نشان داده شده، ادامه می یابد و تمامی مسیرهای ممکن را با ورودی های نمادین بررسی میکند.

2.2 درخت اجرای نمادین (Symbolic Execution Tree)

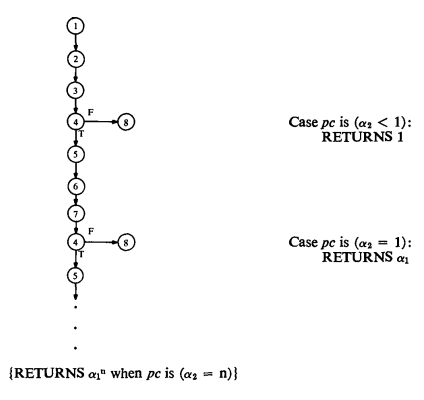
می توان یک درخت اجرا تولید کرد که مسیرهای طی شده در طول اجرای نمادین یک رویه را مشخص کند. به هر دستور اجرا شده یک گره نسبت داده میشود (با برچسب شماره دستور)، و برای هر انتقال میان دستورات یک یال جهت دار رسم میگردد که گره های مربوطه را به هم متصل میکند. در اجرای هر دستور شرطی IF که مسیرها منشعب می شوند، گره مربوطه دارای دو یال خروجی است که به ترتیب با T (TRUE / THEN) و F (FALSE / ELSE) برچسب گذاری میشوند. همچنین وضعیت کامل اجرای برنامه، شامل مقادیر متغیر ها، شمارنده دستورات و شرط مسیر (pc) به هر گره نسبت داده میشود. درخت اجرای برنامه POWER(a₁, a₂) در شکلهای ۴ و ۵ به صورت کامل در شکل ۶ ارائه شده است.

شرط های مسیر (path conditions) که به این شیوه از اجرای نمادین شکل می گیرند، دارای ویژگی های جالب زیر هستند:

وجود ورودی واقعی متناظر:
برای هر برگ پایانی در درخت، که مسیر اجرای کامل را نشان می دهد، همواره یک ورودی غیر نمادین واقعی وجود دارد که اگر برنامه با آن اجرا شود، همان مسیر دستورات اجرا شده را طی خواهد کرد. به عبارت دیگر، هیچ pc‌ای به طور مطلق نادرست (false) نمیشود. استدلال کوتاهی برای این موضوع در پایان بخش ۲ ارائه شده است.
تمایز شرط های مسیر:
شرط های مسیر (pc) مربوط به هر دو برگ پایانی درخت متمایز هستند، برای مثال:

				
					(¬pc1 ∧ pc2)

یعنی دو مسیر که از ریشه مشترک درخت اجرا به دو برگ نهایی منتهی می شوند، دارای یک گره منشعب کننده یا انشعاب یکتا هستند که در آن نقطه مسیرها از یکدیگر جدا می گردند .در آن گره انشعاب، یک گزاره ‎q‎ به یکی از شرط های مسیر افزوده شده و گزاره ‎¬q‎ (نفیِ آن) به دیگری اضافه می شود. از آنجا که هیچ یک از شرط های مسیر ناسازگار (False) نمیشوند، این تمایز منطقی میان آن دو شرط حفظ می گردد.

نکته عملی:

در اجرای برنامه SUM(1, 3, 5):

خط تیره (-) نشان دهنده مقادیری است که تغییری نکرده اند و همانند مقدار خط بالاتر باقی مانده اند.
علامت سؤال (?) نمایانگر مقادیری است که تعریف ‌نشده یا مقدار دهی نشده هستند.

شکل ۳. اجرای نمادین برنامه SUM(a₁, a₂, a₃). شرط مسیر با اختصار pc نشان داده شده است.

توجه: دستورات DO برای ساده‌ سازی معرفی شده‌ اند. این دستورات می توانند به راحتی به حلقه های IF/GOTO تبدیل شوند تا با نماد گذاری های ارائه شده در بخش ‌های قبلی مطابقت پیدا کنند.

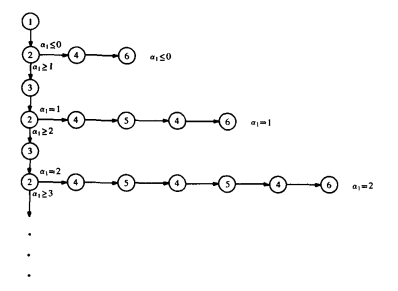
درخت اجرای برنامه TWOLOOPS (شکل ۷) در شکل ۸ نمایش داده شده است. حتی اگر دستور ۴ از حلقه دوم همان پتانسیل انشعابی نحوی را داشته باشد که دستور ۲ از حلقه اول دارد، فرض هایی که هنگام منشعب شدن در دستور ۲ اتخاذ شده ‌اند، در pc حفظ میشوند و در دستور ۴ مورد استفاده قرار می گیرند. این رویکرد مانع از ایجاد یک منشعب شدن جدید می گردد.

درختهای اجرای نمادین این مقاله با درختهای اجرایی که Patterson برای الگو ها یا طرح های کلی برنامه‌ها در مرجع [13] تعریف کرده، شباهت دارند. همچنین در مرجع [12] نیز درباره‌ درختهای Patterson بحث شده است.

2.3 اجرای نمادین و خاصیت جا به ‌جایی (Commutativity)

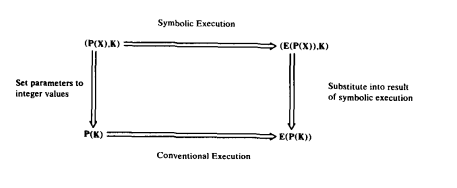
اجرای نمادین تعریف شده برای این زبان ساده اعداد صحیح، دارای ویژگی جالب جا به ‌جایی است. عملیات تخصیص مقادیر خاص به نمادها {a_i}، مثلاً {j_i}، و عملیات اجرای برنامه قابل تعویض هستند.

به عبارت دیگر، اگر برنامه‌ ای با یک مجموعه مشخص از اعداد صحیح {j_i} به ‌صورت معمول اجرا شود (ابتدا تخصیص یا مقدار دهی اولیه a_i توسط j_iو سپس اجرای برنامه)، نتایج با حالتی که ابتدا برنامه به ‌صورت نمادین اجرا شود و سپس نتایج نمادین با مقادیر واقعی جایگزین گردند، کاملاً یکسان خواهد بود یا به عبارت دیگر نتایج، همان نتایجی خواهند بود که در اجرای نمادین برنامه به ‌دست می آید و سپس نتایج نمادین تخصیص داده می شوند )یعنی j’s ها به a’s ها اختصاص می یابند).

منظور از «جایگزینی نتایج نمادین» این است که برای هر برگ پایانی در درخت اجرا، مقادیر a’s (تمام a ها یا تمام عناصر مروبوط به a) برای j’s در تمام متغیرهای برنامه و در شرط مسیر (pc) جایگزین شوند. سپس «نتایج» همان مقادیر برگ پایانی هستند که شرط مسیر آن true شود.

این خاصیت جا به جایی در شکل ۹ نشان داده شده است، که در آن P نشان دهنده برنامه است، E(P(X)) نتیجه اجرای برنامه P بر روی ورودی های X است، و K مجموعه ای از ورودی های صحیح مشخص است.

طبیعتاً همین ویژگی جا به جایی است که اجرای نمادین را مهم و جذاب می سازد. اجرای نمادین دقیقاً همان اثرات اجرای معمولی را ثبت می کند. این روش صرفاً یک تعریف دلخواه جایگزین اجرای برنامه نیست، بلکه گسترشی طبیعی از تعریف معمولی به شمار می رود. همانند رابطه حساب و جبر، محاسبات خاص (حسابی) که توسط عملگر های برنامه تعیین می شوند، به صورت نمادین تعمیم یافته و «به تأخیر» افتاده با استفاده از فرمول های جبری مناسب مورد پردازش قرار می گیرند.

2.4 یک سامانه تعاملی اجرای نمادین — EFFIGY

نویسنده و همکارانش در حال توسعه یک سامانه تعاملی اجرای نمادین به نام EFFIGY بوده اند. کار بر روی این سامانه از اوایل سال ۱۹۷۳ آغاز شده و همچنان در حال پیشرفت است. این سیستم مجموعه ای از خدمات متنوع را در اختیار کاربر قرار میدهد.

امکانات پایه ای برای اشکال زدایی و آزمون برنامه ها برای اجرای نمادین برنامه ها فراهم شده است، به طوری که اجرای معمولی برنامه به عنوان یک حالت خاص قابل استفاده است.
یک مدیر آزمون «جامع» برای کاوش سیستماتیک مسیرهای موجود در درخت اجرای نمادین در دسترس است.
سیستم می تواند نتایج موارد آزمون را به طور خودکار با استنتاج های خروجی بررسی کند، در صورتی که این استنتاج ها ارائه شده باشند.
در نهایت، سامانه دارای یک تأیید گر برنامه است که با استفاده از اجرای نمادین و استنتاج های ارائه شده توسط کاربر، شرایط لازم برای تأیید صحت برنامه را تولید می کند، که به طور کلی بر اساس ایده های Deutsch [4] عمل میکند.

این مقاله بر روی اجرای نمادین به عنوان یک مفهوم مستقل و همچنین بر کاربرد آن در آزمون برنامه ها تمرکز دارد.

2.5 زبان برنامه نویسی قابل استفاده در EFFIGY

زبان مورد استفاده در EFFIGY با هر نسخه جدید سیستم بهبود یافته و اکنون دارای نحو PL/X است که شامل موارد زیر میشود:

رویه های خارجی با قراردادهای انتقال پارامتر PL/I.
متغیرهای دارای مقدار صحیح (فقط FIXED BINARY (31,0)) و آرایه های یک بعدی از اعداد صحیح. این متغیر ها می توانند به صورت STATIC یا AUTOMATIC اعلام شوند و می توانند دارای ویژگی INITIAL باشند.
دستورات انتساب ، دستورات IF (با بندهای THEN و ELSE)، دستورات مرکب با DO…END و دستورات GO TO.
دستورات حلقه ای DO و DO WHILE.
دستورات ابتدایی READ و WRITE.
عملگر های حسابی، رابطه ای و منطقی به صورت انحصاری استفاده می شوند عبارتند از:
- حسابی: +, -, *, /, **, ABS, MOD
- رابطه ای: >, <, >=, <=, =, ≠
- منطقی: & (AND), | (OR), ¬ (NOT), (IMPLIES)

همچنین، مجموعه کامل امکانات تعاملی برای اشکال زدایی نیز در دسترس کاربران است، از جمله:

2.6 امکانات تعاملی اشکال زدایی در EFFIGY

۱. ردیابی یا رهگیری (Tracing):
کاربر می ‌تواند درخواست کند که شماره دستور، متن دستور منبع، نتایج محاسباتی یا ترکیبی از این موارد برای هر دستور یا تمامی دستورات در رویه‌ ها هنگام اجرا نمایش داده شود.

۲. نقاط توقف (Breakpoints):
کاربر میتواند نقاط توقف را قبل یا بعد از هر دستور و یا بین هر جفت دستور قرار دهد. در این نقاط، اجرای برنامه متوقف شده و کنترل به ترمینال کاربر منتقل میشود. کاربر در این حالت میتواند وضعیت اجرای برنامه را بررسی، مقادیر متغیر ها را تغییر دهد و سپس اجرای برنامه را ادامه دهد.

۳. ذخیره سازی وضعیت (State Saving):
هنگام بررسی مسیرهای مختلف برنامه، کاربر ممکن است بخواهد وضعیت اجرای برنامه را ذخیره کند تا بعداً به آن بازگردد و مسیرهای جایگزین را بررسی کند. برای این منظور دستورات SAVE و RESTORE ارائه شده‌ اند.

ویژگی های خاص و دستورات پایه‌ای اجرای نمادین

کاربر می تواند شناسه های دلخواه را به عنوان ورودی های نمادین برنامه تعریف کند (نمادهای a₁, a₂, …). این کار با قرار دادن شناسه ها در نقل قول های دوگانه (“) و استفاده آنها به جای اعداد صحیح مشخص انجام می شود.

نمونه کاربرد:

				
					CALL SUM(1, 3, 5);       // اجرای معمولی با اعداد صحیح
CALL SUM("A", "B", "C"); // اجرای نمادین با نمادهای A، B، C
CALL SUM("A", 3, 5);     // ترکیبی از اجرای نمادین و معمولی

طبق تعریف اجرای نمادین، هنگامی که دستور IF منشعب پذیر اجرا می شود (هر دو شاخه ممکن باشند)، اجرا به طور موازی روی هر دو مسیر جایگزین THEN و ELSE ادامه می یابد و در نتیجه یک درخت اجرای کامل تولید می شود. برای اکثر برنامه ها، این فرایند می تواند بی نهایت باشد. ساده ترین و شاید عمومی ترین راه حل این مشکل، این است که کاربر به صورت تعاملی مسیر جایگزین را در هر مرحله انتخاب کند. این امکان به صورت پایه ای در EFFIGY ارائه شده است. با استفاده از دستورات SAVE و RESTORE،کاربر میتواند وضعیت اجرا را ذخیره کرده و بعداً به مسیرهای جایگزین بازگردد. این قابلیت به کاربر اجازه می دهد درخت اجرا را از ریشه به هر شکلی که بخواهد پیمایش کند.

هرگاه سیستم با اجرای منشعب یک دستور IF مواجه شود (هر دو مسیر ممکن)، کاربر مطلع می شود و میتواند مسیر مورد نظر را انتخاب کند.

رویه POWER:

				
					POWER: PROCEDURE(X, Y);
        Z ← 1;
        J ← 1;
LAB:    IF Y ≥ J THEN
        DO; Z ← Z * X;
                J ← J + 1;
                GO TO LAB; END;
        RETURN (Z);
END;

تعامل کاربر با دستورات IF در اجرای نمادین

در هنگام اجرای یک دستور IF منشعب پذیر، سیستم به کاربر اجازه می دهد که مسیر دلخواه را انتخاب کند:

تایپ go true: سیستم مسیر THEN را دنبال کرده و شرط مسیر (pc) را مطابق با آن به روزرسانی می کند.
تایپ go false: سیستم مسیر ELSE را دنبال کرده و pc را مطابق با آن تغییر می ‌دهد.
تایپ assume(P); go: در این حالت، P یک گزاره (predicate) است که ابتدا با استفاده از مقادیر فعلی متغیرهای برنامه ارزیابی میشود و سپس به pc افزوده می شود (با عملگر AND هم ‌بسته می شود). دستور go موجب می شود که سیستم دستور IF را مجددا با pc اصلاح شده اجرا کند.

مثال عملی:

فرض کنید متغیر برنامه X مقدار a دارد و شرط مسیر فعلی برابر با a>0 است و دستور IF به شکل زیر است:

هنگام ارزیابی، X>5 به a>5 تبدیل می شود.
با استفاده از شرط مسیر (pc)، انتخاب مسیر برای سامانه غیرقابل تشخیص است (یا به عبارت دیگر سیستم قادر به انتخاب مسیر نیست)، زیرا نه:

در این حالت، سیستم از کاربر می خواهد مسیر را انتخاب کند:

اگر او عبارت “go true” را وارد کند، مقدار شرط مسیر (pc) به ‎a > 5‎ به روزرسانی می شود (که از ترکیب ‎a > 0‎ & ‎a > 5‎ به دست آمده است)، و سپس دستور شماره ‎S₁‎ اجرا می گردد.
اگر او عبارت “go false” را وارد کند، شرط مسیر (pc) به ‎a > 0 ∧ ¬(a > 5)‎ به روزرسانی می شود و سپس دستور شماره ‎2‎ اجرا می گردد. اگر او عبارت “assume (“a” > 10); go” را وارد کند، ‎ pc‎ به ‎a > 10‎ (یعنی ‎a > 0 ∧ a > 10‎) تغییر می یابد و دستور IF مجدداً اجرا می شود. این بار

شرط مذکور این بار درست است و اجرای برنامه به دستورS₁ ادامه می یابد. کاربر می توانست همان نتیجه را با وارد کردن دستور “assume (X > 10); go” نیز به دست آورد، زیرا عبارت ‎X > 10‎ در همان گام نخست به ‎a > 10‎ ارزیابی می شود.

2.7 ویژگی‌های تعامل با IF

زمانی که سیستم از کاربر برای انتخاب مسیر در یک IF منشعب ‌پذیر درخواست میکند، وضعیت برنامه همانند حالتی است که اجرای برنامه با یک نقطه توقف قبل از IF متوقف شده باشد.
پیش از تایپ دستورات go true، go false یا go، کاربر می تواند متغیرهای برنامه را بررسی، نقاط توقف اضافه و تنظیمات ردیابی را تغییر دهد.

2.8 اجرای دستور ASSUME

تعریف دستور ASSUME مستقل از IF است و می تواند در هر نقطه ای از برنامه یا در نقاط توقف وارد شود:

ارزیابی عبارت منطقی ASSUME
الحاق نتیجه به شرط مسیر فعلی (pc)، در صورتی که ناسازگار نباشد

می توان از دستور ASSUME در ابتدای یک رویه استفاده کرد، برای مثال، به ‌منظور جلوگیری از در نظر گرفتن ورودیهایی که سیستم برای آنها طراحی نشده است. بحث مطرح شده در بخش ۲ به منظور سادگی آموزشی محدود به چند جمله ای های صحیح بود. شکل ‌های استاندارد(Canonical) برای چند جمله ای ها شناخته ‌شده هستند و همچنین این حقیقت که مجموعه چند جمله ای ها نسبت به جمع و ضرب بسته است، شناخته شده است. تعمیم از حساب به جبر در این مورد به خوبی قابل درک است. سیستم EFFIGY به گونه ‌ای پیاده ‌سازی شده است که بتواند با کلاس ‌های عمومی ‌تر عبارات که پیشتر توصیف شد، کار کند. بدیهی است که تمایل وجود دارد تا سیستمی مانند EFFIGY بر روی زبانهای برنامه ‌نویسی رایج مانند PL/I عمل کند، که این امر بار سنگینی بر بخش دستکاری و ساده سازی فرمولها در سیستم وارد می کند. این بخش از سیستم EFFIGY در واقع از یک برنامه تأییدگر که پیشتر توسط نویسنده ساخته شده بود، اقتباس شده است. قابلیت ها و محدودیت های دستکاری فرمول در EFFIGY مستقیماً از همان سیستم پیشین به ارث رسیده اند که در [9] به تفصیل مورد بحث قرار گرفته است.

2.9 یک مثال دیگر

توصیف کوتاهی از سامانه پایه EFFIGY نیز در منبع ‎[10]‎ ارائه شده است. آن مقاله شامل یک نمونه اسکریپت از یک نشست واقعی با سامانه EFFIGY به عنوان پیوست است، که ممکن است برای برخی از خوانندگان جالب باشد.
در ادامه، توضیحی درباره نحوه آزمون برنامه شکل ۱۰ (SEARCH) در سامانه EFFIGY ارائه می شود. این گام ها قابل اجرا هستند و در واقع بر روی سامانه EFFIGY نیز اجرا شده اند.

برنامه SEARCH برای انجام جستجو دودویی (binary search) بر روی آرگومان ‎X‎ در آرایه ‌ای ‎A‎ از عناصر مرتب ‌شده به ترتیب صعودی ذخیره شده‌ اند، نوشته شده است. دامنه جستجو محدود است.

شکل ۵. اجرای نمادین برنامه POWER(a₁, a₂):

جستجو به عناصر آرایه ای محدود می شود که اشتراک (subscripts) آنها از ‎L‎ تا ‎U‎ (شامل ‎U) است.
اگر تطابقی یافت شود، مقدار زیرنویس عنصری از آرایه که با ‎X‎ برابر است، در متغیر ‎J‎ بازگردانده می شود و مقدار ‎FOUND‎ برابر با ‎1‎ قرار می گیرد. در غیر این صورت، مقدار ‎FOUND‎ برابر با ‎0‎ تنظیم می شود و ‎J‎ مقداری می گیرد که در آن ‎A(J) < X < A(J+1)‎ برقرار باشد.

درخت اجرای نمادین (symbolic execution tree) برای این برنامه بینهایت است، زیرا مقدار اولیه ‎(U – L)‎ می تواند به صورت دلخواه بزرگ انتخاب شود.

اولین آزمایش از برنامه SEARCH ممکن است به صورت زیر انجام شود:

				
					CALL SEARCH (A, 1, 5, "X", FOUND, J);

فرض کنید عناصر آرایه ‎A‎، یعنی ‎A(1)‎، ‎A(2)‎، …، ‎A(5)‎، به مقادیر نمادین “A(1)”، “A(2)”، …، “A(5)” مقداردهی شده باشند. ثابت ‌های ‎1‎، ‎5 و ‎“X”‎ به ‌عنوان آرگومان های ورودی در نظر گرفته می شوند، و متغیرهای ‎FOUND‎ و ‎J‎ از نوع عدد صحیح (integer) هستند که نتایج حاصل از اجرای برنامه SEARCH را باز میگردانند. اجرای نمادین تا رسیدن به دستور شماره ‎7‎ ادامه می ‌یابد؛ در این نقطه، از کاربر پرسیده می ‌شود که آیا ‎“X” = “A(3)”‎ برقرار است یا خیر. اگر کاربر در پاسخ به پرسش سامانه عبارت “save; go true” را وارد کند، وضعیت فعلی اجرا به عنوان وضعیت شماره ۱ ذخیره می شود و اجرای برنامه تا پایان ادامه می یابد. در این حالت، مقادیر به دست‌ آمده عبارت اند از:

				
					‎pc = ("X" = "A(3)")‎، ‎FOUND = 1‎، و ‎J = 3‎.

اکنون کاربر می ‌تواند با وارد کردن دستور “restore 1; go false” حالت دیگر را بررسی کند؛ یعنی زمانی که ‎“X” ≠ “A(3)”‎ است. با ادامه این فرایند، کاربر می‌ تواند زیر درخت محدود حاصل از ورودی های ‎1‎ و ‎5‎ را بررسی کند و در این حالت، یازده گره انتهایی (terminal leaves) را بیابد.

J	FOUND	pc
3	1	X = A (3)
1	1	X = A (1) & X < A (3)
0	0	X < A (1) & X < A (3)
2	1	X = A (2) & X > A (1) & X < A (3)
1	0	X > A (1) & X > A (2) & X < A (3)
2	0	X > A (1) & X > A (2) & X < A (3)
4	1	X = A (4) & X > A (3)
3	0	X > A (3) & X < A (4)
5	1	X = A (5) & X > A (3) & X > A (4)
4	0	X = A (3) & X > A (4) & X > A (5)
5	0	X = A (3) & X > A (4) & X > A (5)

کاربر همچنین می‌ تواند باعث شود سامانه این یازده خروجی را به‌ طور خودکار تولید کند، با استفاده از قابلیت TEST در سامانه EFFIGY:

				
					TEST (200) SEARCH (A, 1, 5, "A", FOUND, J)

عدد ۲۰۰ برای محدود کردن جستجو جامع در درخت اجرای نمادین استفاده می‌ شود، به ‌گونه ‌ای که تنها مسیرهایی که کمتر از ۲۰۰ دستور اجرا می ‌شوند بررسی شوند. در این حالت، این محدودیت لازم نیست زیرا درخت محدود و کوچک است.
این تست شواهدی ارائه می ‌دهد که برنامه قادر است به‌ طور موفقیت ‌آمیز هر عنصر آرایه را پیدا کند. گام بعدی می تواند به شکل زیر باشد:

				
					CALL SEARCH (A, "N", "N" + 4, "X", FOUND, J)

که تعمیمی از تست قبلی است. همانطور که پیشتر، این اجرا در صورت پیگیری جامع، یازده حالت انتهایی مشابه موارد قبلی تولید خواهد کرد، با این تفاوت که 1 با N جایگزین می شود و 2 با N+1 جایگزین می شود، و غیره. برای مثال، حالت دوم فهرست شده در بالا به شکل زیر تبدیل خواهد شد:

شکل ۶. درخت اجرای برنامه POWER(a₁, a₂):

این آزمایش اطمینان بیشتری به ما می دهد که هیچ ویژگی خاصی از اعداد ۱، ۲، …، ۵ (مانند توان های عدد ۲ بودن) بر نتایج پیشین ما تأثیر نگذاشته است.

آزمایش مشابه دیگری، اما با حالتی خاص‌تر، به صورت زیر است:

				
					CALL SEARCH (A, "N", "N", "X", FOUND, J)

که در صورت بررسی جامع، یک درخت با سه گره پایانی (three-leaf tree) ایجاد می‌کند.

pc	FOUND	J
X= A(N)	1	N
X< A(N)	0	N-1
X> A(N)	0	N

دو فراخوانی زیر:

				
					CALL SEARCH (A, 1, "N", "X", FOUND, J)
CALL SEARCH (A, "U", "U", "X", FOUND, J)

کلی ترین آزمایشها محسوب می شوند و می توان از آنها برای بررسی صحت عملکرد در فرآیندهای میانگین گیری کران ها (bounds averaging) و کاهش دامنه کران ها (bounds shrinking) استفاده کرد.

اگرچه هر دو فراخوانی به درختهای اجرای نمادین بی نهایت منجر میشوند، اما نتایج جالبی مانند مورد زیر — که از فراخوانی نخست به دست آمده — قابل استخراج است:

J	FOUND	pc
(N+1)/2	1	X = A ((N+1)/2) & N> 0
((N+1)/2)/2)	1	X = A (((N+1)/2)/2) & N > 0 & X < A ((N+1)/2) & (N+1)/2>1
((N+1)/2+N+1)/2	1	X > A ((N+1)/2) & N>0 & X=A(((N+1)/2+N+1)/2) & (N+1)/2<N

توجه کنید که در جریان انجام تمام این آزمون ها، هیچ مقدار واقعی یا مشخصی برای آرایه A یا آرگومان X ارائه نمیشود؛ بلکه همه‌ آنها به صورت نمادین در نظر گرفته می شوند. ویژگیهای مهم این مقادیر (مانند رابطه X ≤ A(N)) در فرایند اجرای نمادین آشکار می گردند. تمامی این آزمایشها تنها بر پایه برنامه اصلی انجام میشوند و نیازی به تعریف گزاره های درستی (correctness predicates) نیست. چنانکه در بخش ۸ به تفصیل بیان خواهد شد، میتوان گزاره های ورودی، خروجی، استقرایی و بررسی کننده را در کنار اجرای نمادین برای آزمون و اثبات درستی برنامه ها به کار گرفت؛ با این حال، چنین گزاره هایی برای آزمون نمادین صرف الزامی نیستند.

در نهایت، همانند اجرای معمولی برنامه، هنگام به‌ کارگیری اجرای نمادین برای آزمون، باید در انتخاب موارد آزمون معنادار و در تعیین مرز کافی بودن آزمون ها دقت کرد. همچون اجرای عادی، هنگام آزمایش برنامه با استفاده از اجرای نمادین نیز باید در انتخاب موارد آزمایشی (test cases) جالب و معنادار و در تعیین نقطه کفایت (deciding when enough is enough) آزمایش ها دقت کافی به عمل آید.

2.10 درستی برنامه، اثبات ها و اجرای نمادین

برای اثبات درستی یک برنامه به کمک روشی که فلوید (Floyd) در [6] معرفی کرده است، برنامه نویس باید دو گزاره را همراه با برنامه ارائه کند: یکی گزاره ورودی و دیگری گزاره خروجی.
این دو گزاره رفتار «درست» برنامه را تعریف می کنند. برنامه زمانی «درست» محسوب می شود که برای همه ورودی هایی که گزاره ورودی را برآورده میسازند، خروجی های تولید شده (در صورت وجود) نیز گزاره خروجی را برآورده کنند. فلوید روشی را برای بررسی سازگاری میان برنامه و گزاره های ورودی/خروجی آن و در نتیجه اثبات درستی برنامه ارائه کرده است.

یکی از مراحل اصلی در روش فلوید، تولید شرایط اثبات (Verification Conditions) است که میتوان آن را به سادگی از طریق اجرای نمادین مسیرهای برنامه به دست آورد. دویچ (Deutsch) به طور مستقل مفهوم اجرای نمادین را در جریان توسعه سامانه تعاملی اثبات‌ کننده برنامه خود [4] ابداع کرد و از این روش برای تولید شرایط اثبات بهره گرفت.

برای توضیح ساده تر این روش، میتوان از سه دستور کمکی در زبان برنامه سازی استفاده کرد: ASSUME، PROVE و ASSERT که برای پیوند دادن گزاره ها به بخش های مختلف برنامه به کار می روند.
هر سه دستور شامل یک فرمول منطقی هستند که در پرانتز پس از نام دستور قرار می گیرد؛ برای نمونه:
ASSERT(X > 0) در این فرمول ها، متغیرهای آزاد همان متغیرهای برنامه فرض می شوند. دستور ASSUME(B) که در بخش ششم تعریف شد، هنگام اجرا، گزاره B را با استفاده از مقادیر فعلی متغیرهای برنامه ارزیابی کرده و نتیجه حاصل را به شرط مسیر (pc) می افزاید، یعنی:

				
					pc ←pc ∧ value(B)

دستور PROVE(B) با تشکیل عبارت:

				
					pc ⊃ value(B)

اجرا می شود و می کوشد بررسی کند که آیا این عبارت یک قضیه منطقی است یا نه، و سپس نتیجه (درست یا نادرست) را نمایش میدهد. در کاربردهایی که در ادامه می آید، همین عبارات در واقع همان شرایط اثبات فلوید خواهند بود.
دستور ASSERT بسته به جایگاه خود در برنامه، می تواند همانند یک ASSUME یا یک PROVE عمل کند.

علاوه بر گزاره های آغازین و پایانی که درستی کلی برنامه را مشخص می کنند، روش فلوید نیازمند افزودن گزاره های استقرایی (Inductive Predicates) در نقاط مختلف برنامه است. معمولاً دست کم یک گزاره استقرایی در هر حلقه قرار داده می شود، هرچند نحوه جایگذاری آنها آزاد است، به شرط آنکه مسیرهای کنترل بین دو گزاره طول محدودی داشته باشند. این گزاره های استقرایی امکان می دهند که استدلال کلی اثبات به صورت استقرایی انجام گیرد و در نتیجه، اثبات درستی کل برنامه به اثبات درستی مجموعه ‌ای محدود از مسیرهای محدود کاهش یابد.

فرض کنید گزاره‌ های ورودی، خروجی و استقرایی با استفاده از دستورهای ASSERT در نقاط مناسب برنامه جایگذاری شده‌ اند (برای مثال گزاره ورودی در ابتدای برنامه با یک ASSERT مشخص شده است). در این صورت، مجموعه‌ ای محدود از مسیرهای برنامه در اختیار داریم که هر یک با یک ASSERT آغاز و با یک ASSERT پایان می یابد و باید درستی هر مسیر جداگانه بررسی شود.
به بیان دیگر، باید نشان داد که با هر مجموعه از مقادیر متغیرها که گزاره آغاز مسیر را برآورده می کنند، اجرای مسیر منتهی به مقادیری میشود که گزاره پایانی را نیز برآورده می سازند.

درستی هر مسیر را می توان با اجرای نمادین به شکل زیر اثبات کرد:

دستور ASSERT آغاز مسیر را به ASSUME و دستورASSERT پایان مسیر را بهPROVE تبدیل کنید.
مقدار شرط مسیر را برابر «درست» قرار دهید و همه متغیرهای برنامه را با نمادهای متمایز (مانند a₁، a₂ و …) مقدار دهی کنید.
مسیر را به صورت نمادین اجرا کنید. هرگاه به یک دستور شرطی IF برسید که نتیجه اش نامعین است، با انتخاب «go true» یا «go false» مسیر مورد نظر را دنبال کنید.
اگر در پایان مسیر، اجرای دستور PROVE مقدار «درست» را نمایش دهد، مسیر صحیح است؛ در غیر این صورت، نادرست است.

در صورتی که اجرای نمادین خاصیت جا به‌ جایی (commutativity) که در بخش پنجم توضیح داده شد را داشته باشد، می توان به ‌روشنی دریافت که این شیوه، روشی معتبر برای اثبات درستی برنامه است.

در این روش، اثبات برنامه بر پایه مقادیر متغیرهای آن در ابتدای مسیر انجام می شود؛ مقادیری که به‌ صورت نمادین نامگذاری شده‌ اند. شرط مسیر (pc) به ‌تدریج فرض ‌هایی را که درباره این مقادیر اولیه به ‌کار می ‌روند، در خود جمع می کند. اجرای نخستین دستور ASSUME، فرض‌ های لازم درباره مقادیر آغازین را در شرط مسیر ثبت می‌کند. فرمول ‌هایی که در نتیجه اجرای دستورهای انتساب حاصل می ‌شوند، مقادیر جدید متغیر ها را به‌ عنوان تابعی از مقادیر آغازین بیان می ‌کنند. همچنین، اجرای دستورهای شرطی نامعین، فرض‌ های اضافی مورد نیاز برای ادامه مسیر خاص را به شرط مسیر می افزاید.

در نهایت، اجرای دستور PROVE در پایان مسیر، گزاره ‌ای را به ‌عنوان کاندیدای قضیه (شرط اعتبار (verification condition)) ایجاد می کند؛ این گزاره در واقع این پرسش را بیان می کند که:

با فرض آنکه گزاره آغازین برقرار بوده و اجرای برنامه مطابق این مسیر (ثبت ‌شده در pc) پیش رفته است، آیا مقادیر کنونیِ متغیرهای برنامه در انتهای مسیر، گزاره پایانی را نیز برقرار می کنند؟

شکل 7. رویه دو حلقه‌ای:

				
					TWOLOOPS: PROCEDURE (N);
	DO J=1 TO N;
	   (body of statements) END;
	DO K = 1 TO N;
	   (body of statements) END;
	END;

شکل ۸. درخت اجرا برای روال TWOLOOPS:

شکل 9. نمودار جابجایی:

شکل 10. رویه SEARCH:

				
					SEARCH:
	PROC(A, L, U, X, FOUND, J);
	DCL A(*) INTEGER;
	DCL (L, U, X, FOUND, J) INTEGER;
	FOUND = 0;
	DO WHILE (L ¬ &gt; U &amp; FOUND = 0);
		J = (L + U)/2;
		IF X = A(J) THEN FOUND = 1
			ELSE IF X &lt; A(J)
				THEN U = J-1
				ELSE = J+1;
	END;
	IF FOUND = 0 THEN J = L-1;
END;

با در اختیار داشتن یک سامانه اجرای نمادین مانند EFFIGY، از نظر مفهومی بسیار ساده است که بتوان آن را برای اثبات درستی برنامه نیز به کار برد، تنها با افزودن یک دستور PROVE و یک کنترل ‌کننده مدیریتی برای شمارش مسیرها و اعمال تصمیمات مسیر در اجرای دستورهای شرطی نامعین (IF). ما این کار را انجام داده ‌ایم و از آن به ‌عنوان ابزاری برای پیشبرد پژوهش در زمینه تکنیک‌ های اثبات درستی استفاده می کنیم.

در واقع، مفاهیم اثبات درستی برنامه و اجرای نمادین از نظر مفهومی و ابزارهای مورد نیاز برای اجرا به‌شدت به یکدیگر مرتبط هستند. فرض کنید گزاره‌ های ورودی/خروجی فلوید را با قرار دادن گزاره ورودی به‌ صورت دستور ASSUME در ابتدای برنامه و گزاره خروجی به ‌صورت دستور PROVE در انتهای برنامه به برنامه پیوند داده‌ ایم. با تعریفی که برای دستور ASSUME ارائه شد، این ASSUME اولیه تحلیل بعدی، چه اجرای نمادین و چه اثبات درستی، را محدود به مقادیری میکند که گزاره آغازین را برآورده می‌ سازند.
به ‌کارگیری تعریف PROVE برای اثبات درستی، همچنین در آزمون برنامه با اجرای نمادین بسیار مفید است. در آزمون برنامه، چه به‌ صورت نمادین و چه عادی، باید خروجی تولید شده بررسی شود و درستی آن سنجیده شود. اگر معیار درستی را به‌صورت یک گزاره خروجی فرمالیزه (formalize) کرده و در انتهای برنامه با دستور PROVE قرار دهیم، سامانه اجرای نمادین نیز بررسی صحیح نتایج آزمون را انجام خواهد داد.

یک نکته دیگر درباره تعریف دستور PROVE است. برخی زبان ها از بررسی زمان اجرا برای گزاره های برنامه پشتیبانی می کنند، مثلاً با استفاده از دستور ASSERT (مانند Algol W [14]). این دستورات را میتوان به سادگی با در نظر گرفتن: ASSERT(B).

به عنوان اختصار برای:

				
					IF ¬B THEN
(چند پیغام خطا از جمله  SIGNAL ERROR)

پیاده سازی کرد. از آنجا که این یک دستور IF عادی است، میتوان اجرای نمادین آن را نیز در نظر گرفت. اگر برنامه درست باشد، اجرای دستور IF همواره باید به مسیر غیرواقعی (False) ختم شود. طبق تعریف اجرای نمادین IF، این فقط زمانی اتفاق می افتد که:

				
					pc ⊃ value(B)

دقیقاً همان چیزی است که PROVE تلاش میکند اثبات کند!

برای هر برنامه ‌ای که درخت اجرای نمادین آن متناهی باشد و معیارهای درستی آن با گزاره ‌های ورودی/خروجی صریح شده باشد، اجرای نمادین کامل و اثبات درستی به همان فرایند ختم می ‌شود. از آنجا که گزاره‌ های استقرایی لازم نیست، مجموعه مسیر هایی که نیاز به اثبات دارند، همان مسیرهای بین گزاره ورودی و گزاره خروجی هستند که توسط درخت اجرای متناهی توصیف می ‌شوند.

برای برنامه‌ هایی که درخت اجرای آنها نامتناهی است، آزمون نمادین نمی ‌تواند کامل باشد و هیچ اثبات قطعی برای درستی ارائه نمی ‌دهد. یک روش واضح برای گسترش اجرای نمادین و ارائه اثبات درستی در همه موارد، استفاده از نوعی استدلال استقرایی بر بخش ‌های نامتناهی درخت است. این دقیقاً همان کاری است که روش اثبات درستی فلوید انجام می ‌دهد. گزاره ‌های استقرایی قرار داده ‌شده در حلقه‌ ها، کمک استقرایی لازم را برای اجرای نمادین روی شاخه‌ های نامتناهی فراهم می ‌کنند. رویکردی مشابه اما متفاوت نیز اخیراً توسط Topor و Burstall [15] ارائه شده است تا کمک استقرایی لازم برای پیمایش شاخه ‌های نامتناهی و اثبات درستی فراهم شود.

یک تفاوت مهم بین اجرای نمادین برای آزمون برنامه و اجرای نمادین برای اثبات درستی وجود دارد: توانمندی لازم برای مدیریت گزاره ‌ها در اثبات درستی بسیار بالاتر است. اگر صرفاً به اجرای نمادین محدود شویم و از گزاره‌ های معرفی ‌شده توسط کاربر استفاده نکنیم، pc و عبارات مورد اثبات به ‌صورت نحوی و معنایی توسط زبان برنامه ‌نویسی تعیین می ‌شوند. اما در اثبات درستی، معنای گزاره‌ ها از مسأله برنامه ناشی می ‌شود و نه از زبان برنامه ‌نویسی.

این تفاوت نشان می ‌دهد که اجرای نمادین برای آزمون برنامه‌ها در کوتاه ‌مدت، تکنیکی قابل بهره ‌برداری ‌تر و عملی ‌تر نسبت به روش عمومی تر اثبات برنامه است.

2.11 مسائل یا ملاحظات عملی

بسیاری از مسائل عملی که در سامانه ‌های اثبات درستی برنامه ‌ها ایجاد می شوند، در اجرای نمادین نیز مشاهده می ‌شوند. برای مثال، یکی از مشکلات مشترک در هر دو حوزه، یافتن روش عملی برای مدیریت ارجاعات حافظه و متغیر ها است. به‌ عنوان نمونه، نمادگذاری آرایه ‌ای مانندA(I) بسته به مقدار I به عنصر خاص متفاوتی از آرایه A اشاره می ‌کند. زمانی که مقدار I یک عبارت نمادین باشد، عنصر خاص مورد ارجاع تابعی از ورودی‌ های اولیه برنامه خواهد بود. در بسیاری از موارد، حتی با بررسی تمامی اطلاعات موجود در مورد این ورودی‌ ها که درpc نگهداری می شود، ارجاع خاص ممکن است به طور ذاتی نامشخص و مبهم باشد.

حداقل دو روش برای مواجهه با این مشکل وجود دارد، اگرچه هیچ یک کاملاً رضایت بخش نیستند:

میتوان تحلیل موردی جامع انجام داد، همانطور که در اجرای نامعین دستورهای شرطی (IF) انجام می شود.
میتوان ابهام را بدون حل شدن باقی گذاشت اما با ذخیره مقادیر شرطی متغیرها حفظ کرد. برای مثال، مقدار( A(I) با فرض اینکه مقدار I برابر با i است) ممکن است به شکل زیر ذخیره شود:

اگر i = 1 باشد آنگاه x، در غیر اینصورت اگر i = 3 باشد y، در غیر اینصورت اگر i = j + 1 باشد z …

تعارض میان جنبه ‌های گسسته حساب کامپیوتری و ماهیت پیوسته اعداد حقیقی با دقت نامتناهی نیز یکی دیگر از مسائل اجرای نمادین است. برای کمک به اثبات قضایا و افزایش خوانایی فرمول ها، لازم است آنها تا حد امکان ساده سازی شوند. با این حال، بسیاری از ساده ‌سازی های قدرتمند ممنوع می ‌شوند اگر اصرار بر این باشد که عبارات حاصل، همان مقادیر را هنگام ارزیابی توسط کامپیوتر تولید کنند، زیرا در غیر این صورت خاصیت جابجایی که در بخش ۵ بحث شد، نقض می شود.

همچنین، فاصله ‌ای بین درستی یک گزاره و توانایی اثبات خودکار صحت آن توسط سامانه اثبات قضایا وجود دارد. به طور خاص، یک سامانه خودکار ممکن است نتیجه بگیرد که اجرای برخی از دستورهای IF نامشخص است در حالی که در واقع چنین نیست. در این حالت، سامانه مسیری را دنبال می کند که هرگز در اجرای واقعی قابل پیمایش نیست. بنابراین، ادعای پیشین که pc هرگز نادرست نمی شود، که در پایان بخش ۲ بیان شد، دیگر قابل بیان نیست.

البته، حتی برای زبان های برنامه ‌نویسی نسبتاً ساده، اثبات قضایا لازم برای اجرای نمادین برنامه‌ ها در آن زبان از نظر نظری غیرممکن می شود. به عبارت دیگر، ساخت یک سامانه اثبات قضیه که بتواند صحت یا کذب این کلاس از عبارات را تعیین کند، امکان ‌پذیر نیست.

3. نتیجه گیری

ایده اجرای نمادین یک برنامه ارائه شد که ارتباط نزدیکی با مفهوم معمول اجرای برنامه دارد. این روش این مزیت را دارد که یک اجرای نمادین میتواند نماینده تعداد زیادی، و اغلب بینهایت، از اجراهای عادی باشد. این قابلیت در آزمون و عیب یابی برنامه ها بسیار مفید است. سیستم EFFIGY که توسط نویسنده و همکارانش توسعه یافته، نیز معرفی شد. این سیستم اجرای نمادین را در یک محیط تعاملی چند منظور برای اشکال زدایی فراهم می کند. امکانات اضافی مبتنی بر قابلیت اجرای نمادین شامل مدیر آزمون «جامع» و تأیید کننده برنامه است. سیستم های تعاملی برای اشکال زدایی و آزمون ابزارهای قدرتمند و مفیدی در توسعه برنامه ها محسوب می شوند و افزودن ویژگی های مبتنی بر اجرای نمادین به آنها، پیشرفتی قابل توجه است، ضمن آنکه امکانات معمول همچنان به عنوان حالت ویژه در دسترس اند.

اجرای نمادین همچنین در دیگر اشکال تحلیل برنامه، از جمله تولید داده های آزمون و بهینه سازی برنامه ها، مفید است. یک سیستم اجرای نمادین مانند EFFIGY مسیر طبیعی برای رشد سیستم های کنونی فراهم می کند و امکان دستیابی تدریجی به سیستم های تأیید برنامه در آینده را می دهد. داشتن یک سیستم در حال اجرا که بتوان آن را به صورت تدریجی بهبود داد، تجربه و پشتیبانی ارزشمندی برای کاربران فراهم می کند. اگرچه استفاده عملی از سیستم EFFIGY هنوز محدود است، اما بینش قابل توجهی در مورد مفهوم کلی اجرای نمادین و کاربردهای متنوع آن در طول ساخت این سیستم به دست آمده است.

از همکاری‌های A.C. Chibib, J.A. Darringer، و S.L. Hantler که به ایده ها و طراحی و پیاده سازی سیستم EFFIGY کمک شایانی کرده اند، سپاسگزاری می شود. همچنین قدردانی از M.W. Blasgen, S.L. Hantler، و J.R. Buchanan برای ارائه نقدهای سازنده و دقیق درباره پیش نویس های اولیه این گزارش، و از D.P. Rozenberg, P.C. Goldberg، و P.S. Dauber برای حمایت و تشویقشان به عمل آمده است.

تاریخ دریافت: دسامبر ۱۹۷۴؛ بازبینی: ژانویه ۱۹۷۵

4. منابع:

				
					1.	Boyer, R.S., Elspas, B., Levitt, K.N. SELECT—A formal system for testing and debugging programs by symbolic execution. 1975 Int. Conf. on Reliable Software, April 1975, pp. 234-245.
2.	. Clarke, L. A system to generate test data and symbolically execute programs. Rep. No. CU-CS-060-75, Dep. of Computer Sci., U. of Colorado, Feb. 1975.
3.	Darlington, J. A semantic approach to automatic program improvement. Ph.D. Th., U. of Edinburgh, 1972.
4.	Deutsch, L.P. An interactive program verifier. Ph.D. Th., Dep. of Computer Sci., U. of California, Berkeley, May 1973.
5.	Elspas, B., et al. An assessment of techniques for proving program correctness. Computing Surveys 4, 2 (June 1972), 97-147.
6.	Floyd, R.W. Assigning meanings to programs, Proc. Syrup. Appl. Math. Vol. 19, Amer. Math. Soc., Provincetown, R.I., 1967, pp. 19-32.
7.	King, J.C. Proving programs to be correct. IEEE Trans. on Comp. C-20, 11 (Nov. 1971), 1331-1336.
8.	King, J.C. A program verifier. Proc. IFIP Cong. 71, North-Holland, Amsterdam, 1971, pp. 235-249.
9.	King, J.C. and Floyd, R.W. An interpretation oriented theorem prover over integers, J. Computer Syst. Sci. 6, 4(Aug. 1972), 305-323.
10.	King, J.C. A new approach to program testing. 1975 Int. Conf. on Reliable Software, April 1975, pp. 228-233.
11.	H. Krause, K.W., et al. Optimal software test planning through Automated network analysis. IEEE Syrup. on Computer Software Reliability, April 1973, pp. 18-22.
12.	Manna, Z. Mathematical Theory of Computation. McGraw-Hill, New York, 1974, Ch. 4.
13.	Paterson, M.S. Equivalence problems in a model of computation. Ph.D. Th., U. of Cambridge, England, Aug. 1967. Also published as A.I. Tech. Memo No. 1 (Memo No. 211), MIT, Nov. 1970.
14.	Sites, R.L. Algol W Reference Manual. Rep. CS-230 (Clearinghouse No. PB 203601), Computer Sci. Dep., Stanford LI., Feb. 1972.
15.	Topor, R.W., and Burstall, R.M. Verification of programs by symbolic execution—progress report. Unpublished report, Dep. of Machine Intelligence, U. of Edinburgh, Scotland, Dec. 1972.
16.	Urschler, G. Complete redundant expression elimination in flow diagrams. Rep. RC4965, IBM Research, Yorktown Heights, N.Y., Aug. 1974.